题目内容
8．先化简，再求值：$\frac{x^2}{{{x^2}-1}}÷（\frac{1}{x-1}+1）$，其中x是$5-\sqrt{5}$的整数部分．分析 首先将括号里面进行通分，再将能因式分解的进行因式分解，进而化简求出答案．
解答 解：原式=$\frac{{x}^{2}}{（x-1）（x+1）}$÷$\frac{x}{x-1}$
=$\frac{{x}^{2}}{（x-1）（x+1）}$×$\frac{x+1}{x}$
=$\frac{x}{x+1}$，
∵-3＜-$\sqrt{5}$＜-2，2＜5-$\sqrt{5}$＜3，
则x=2，
∴原式=$\frac{2}{3}$．
点评 此题主要考查了分式的化简求值以及估算无理数的大小，正确化简分式是解题关键．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
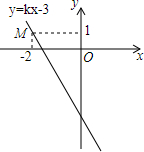如图，已知直线y=kx-3经过点M，求此直线与x轴，y轴形成的三角形的面积．
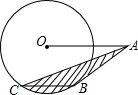如图，⊙O的半径为4，OA=8，AB切⊙O于B，弦BC∥OA，连接AC，则图中阴影部分的面积为$\frac{8}{3}$π．
如图，已知三角形三个顶点的坐标分别为：A（2，-1），B（4，3），C（1，2），请你计算△ABC的面积．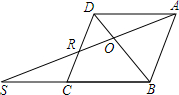
菱形ABCD中，O对角线BD上一点，连接AO并延长，与DC交于点R，与BC的延长线交于点S，若AD=4，∠DCB=60°，BS=10，求CR、OD和AR的长．