题目内容
11.已知$\frac{a}{b}=\frac{c}{d}=\frac{2}{3}$,则$\frac{a+c}{b+d}$=$\frac{2}{3}$.分析 根据比例的性质求出a=$\frac{2}{3}$b,c=$\frac{2}{3}$d,再代入求出即可.
解答 解:∵$\frac{a}{b}$=$\frac{c}{d}$=$\frac{2}{3}$,
∴a=$\frac{2}{3}$b,c=$\frac{2}{3}$d,
∴$\frac{a+c}{b+d}$=$\frac{\frac{2}{3}b+\frac{2}{3}d}{b+d}$=$\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 本题考查了比例的性质的应用,能根据比例的性质求出a=$\frac{2}{3}$b和c=$\frac{2}{3}$d是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.下列命题是真命题的是( )
| A. | 相等的角是对顶角 | B. | 全等三角形的对应角相等 | ||
| C. | 如果x2=1那么x=1 | D. | $\sqrt{4}$是无理数 |
 如图,已知三角形三个顶点的坐标分别为:A(2,-1),B(4,3),C(1,2),请你计算△ABC的面积.
如图,已知三角形三个顶点的坐标分别为:A(2,-1),B(4,3),C(1,2),请你计算△ABC的面积.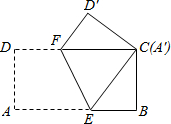 如图,将长8cm,宽4cm的矩形纸片ABCD折叠,使点A与C重合,则DF的长为3.
如图,将长8cm,宽4cm的矩形纸片ABCD折叠,使点A与C重合,则DF的长为3.