题目内容
20.分式$\frac{m}{m+n}$,$\frac{-mn}{{{{(m+n)}^2}}}$,$\frac{n}{m-n}$的最简公分母是( )| A. | (m+n)2(m-n) | B. | (m+n)3(m-n) | C. | (m+n)(m-n) | D. | (m2-n2)2 |
分析 根据确定最简公分母的方法是:
(1)取各分母系数的最小公倍数;
(2)凡单独出现的字母连同它的指数作为最简公分母的一个因式;
(3)同底数幂取次数最高的,得到的因式的积就是最简公分母;即可得出答案.
解答 解:分式$\frac{m}{m+n}$,$\frac{-mn}{{{{(m+n)}^2}}}$,$\frac{n}{m-n}$的最简公分母是(m+n)2(m-n);
故选A.
点评 此题考查了最简公分母,解题的关键是准确求出各个分式中分母的最简公分母,确定最简公分母的方法一定要掌握.

练习册系列答案
相关题目
11.水是万物生命之源,但随着人口急剧增长,水资源透支令人担忧,节约用水迫在眉睫.某城市为了避免居民用水浪费现象,制定了居民每月每户用水标准10m3,收费为正常标准,如果超标用水,超过部分加价收费,下表是小明家2014年两个月的收费表:
请问该城市居民标准内用水及超标用水的价格各是多少元?
| 时间项目 | 用水量(m3) | 费用(元) |
| 11月 | 15 | 35 |
| 12月 | 18 | 44 |
8.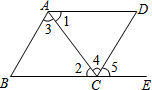 如图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,能判定AB∥CD的条件为( )
如图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,能判定AB∥CD的条件为( )
 如图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,能判定AB∥CD的条件为( )
如图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,能判定AB∥CD的条件为( )| A. | ①②③④ | B. | ①②④ | C. | ①③④ | D. | ①②③ |
12.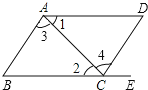 如图,给出下列条件:①∠1=∠2;②∠3=∠4;③AD∥BE,且∠D=∠B;其中,能推出AB∥DC的条件为( )
如图,给出下列条件:①∠1=∠2;②∠3=∠4;③AD∥BE,且∠D=∠B;其中,能推出AB∥DC的条件为( )
 如图,给出下列条件:①∠1=∠2;②∠3=∠4;③AD∥BE,且∠D=∠B;其中,能推出AB∥DC的条件为( )
如图,给出下列条件:①∠1=∠2;②∠3=∠4;③AD∥BE,且∠D=∠B;其中,能推出AB∥DC的条件为( )| A. | ①② | B. | ①③ | C. | ②③ | D. | 以上都错 |
9.根据下列条件,能判断出一个四边形是平行四边形的是( )
| A. | 一组对边相等 | B. | 两条对角线互相垂直 | ||
| C. | 一组对边平行 | D. | 两条对角线互相平分 |