题目内容
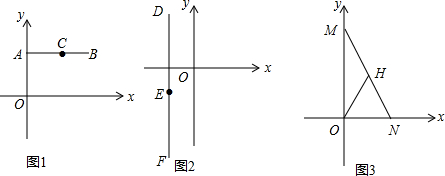
5.阅读:在平面直角坐标系中,以任意两点P(x1,y1)、Q(x2,y2)为端点的线段的中点坐标为($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{y}_{1}+{y}_{2}}{2}$).理解:(1)如图1,C为线段AB的中点,A点的坐标为(0,2),B点的坐标为(4,2),则C点的坐标为(2,2)
(2)如图2,E为线段DF的中点,E点的坐标为(-1,-2),D点的坐标为(-1,3),则F点的坐标为(-1,-7).
应用:如图3,点M的坐标为(0,4),点N的坐标为(2,0),则线段MN的中点H的坐标为(1,2),线段OH的长为$\sqrt{5}$,线段MN的长为2$\sqrt{5}$,$\frac{OH}{MN}$=$\frac{1}{2}$.
扩展:直角三角形ABC中,D为斜边AB的中点,则$\frac{CD}{AB}$=$\frac{1}{2}$(只填数字,不要求证明)
分析 (1)直接应用阅读中的结论即可;
(2)利用应用阅读中的结论建立方程求解即可;
应用:利用阅读中的结论和平面坐标系中两点间的距离公式求解即可;
拓展:应用直角三角形的性质即可得出结论.
解答 解:(1)∵C为线段AB的中点,A点的坐标为(0,2),B点的坐标为(4,2),
∴C(2,2),
故答案为(2,2),
(2)设F(a,b),
∵E为线段DF的中点,E点的坐标为(-1,-2),D点的坐标为(-1,3),
∴-1+a=-2,3+b=-4,
∴a=-1,b=-7,
∴F(-1,-7),
故答案为(-1,-7);
应用:∵点M的坐标为(0,4),点N的坐标为(2,0),
∴线段MN的中点H的坐标(1,2),
∴OH=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∵点M的坐标为(0,4),点N的坐标为(2,0),
∴MN=$\sqrt{(2-0)^{2}+(4-0)^{2}}$=2$\sqrt{5}$,
∴$\frac{OH}{MN}$=$\frac{\sqrt{5}}{2\sqrt{5}}$=$\frac{1}{2}$,
故答案为(1,2),$\sqrt{5}$,2$\sqrt{5}$,$\frac{1}{2}$;
扩展:∵直角三角形ABC中,D为斜边AB的中点,
∴CD=$\frac{1}{2}$AB,
∴$\frac{CD}{AB}$=$\frac{\frac{1}{2}AB}{AB}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 此题是三角形综合题,主要考查了中点坐标的确定,平面坐标系中两点间的距离公式,直角三角形的性质,解本题的关键是中点坐标公式的理解和运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.下列各式的分解因式中,没有用到公式法的是( )
| A. | 3m2-6mn+3n2=3(m-n)2 | B. | x2b+ab2+ab=ab(a+b+1) | ||
| C. | mx2-4m=m(x-2)(x+2) | D. | x2+12x+36=(x+6)2 |
14.已知$\frac{a}{b+c+d}$=$\frac{b}{a+c+d}$=$\frac{c}{a+b+d}$=$\frac{d}{a+b+c}$=k,则k的值为( )
| A. | -1 | B. | 3 | C. | -1或$\frac{1}{3}$ | D. | 4 |
 阅读材料:新定义运算max{a,b}:当a≥b时,max{a,b}=a;当a<b时,max{a,b}=b.例如:max{-3,2}=2请你阅读以上材料,完成下列各题.
阅读材料:新定义运算max{a,b}:当a≥b时,max{a,b}=a;当a<b时,max{a,b}=b.例如:max{-3,2}=2请你阅读以上材料,完成下列各题.