题目内容
10.先化简,再求值:$\frac{1}{m}$+$\sqrt{\frac{1}{{m}^{2}}+{m}^{2}-2}$,其中m=$\frac{1}{6}$.分析 首先根据m的值,利用完全平方公式把根号下的数开方,进一步代入求得答案即可.
解答 解:∵m=$\frac{1}{6}$,
∴$\frac{1}{m}$+$\sqrt{\frac{1}{{m}^{2}}+{m}^{2}-2}$
=$\frac{1}{m}$+$\sqrt{(\frac{1}{m}-m)^{2}}$
=$\frac{1}{m}$+$\frac{1}{m}$-m
=$\frac{2}{m}$-m
=12-$\frac{1}{6}$
=11$\frac{5}{6}$.
点评 此题考查二次根式的化简求值,掌握完全平方公式是解决问题的关键.

练习册系列答案
相关题目
1.已知A(x1,2015),B(x2,2015)是二次函数y=ax2+bx+3(a≠b)的图象上两点,则当x=x1+x2时,二次函数的值是( )
| A. | -$\frac{{b}^{2}}{4a}$+3 | B. | $\frac{2{b}^{2}}{a}$+3 | C. | 2015 | D. | 3 |
 如图,牧马人从A地出发,先到草地边某一处牧马,再到河边饮马,然后回到B处,请画出最短路径.
如图,牧马人从A地出发,先到草地边某一处牧马,再到河边饮马,然后回到B处,请画出最短路径.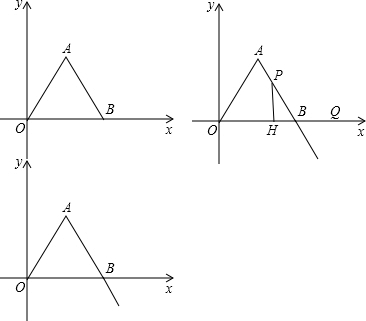
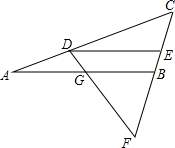 如图,已知DE∥GB.且$\frac{AD}{DG}$=$\frac{AC}{BC}$,求证:△DEF是等腰三角形.
如图,已知DE∥GB.且$\frac{AD}{DG}$=$\frac{AC}{BC}$,求证:△DEF是等腰三角形.