题目内容
15.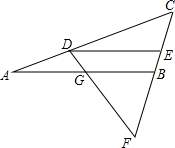 如图,已知DE∥GB.且$\frac{AD}{DG}$=$\frac{AC}{BC}$,求证:△DEF是等腰三角形.
如图,已知DE∥GB.且$\frac{AD}{DG}$=$\frac{AC}{BC}$,求证:△DEF是等腰三角形.
分析 由平行线分线段成比例定理得出比例式$\frac{AD}{BE}=\frac{AC}{BC}$,$\frac{DG}{DF}=\frac{BE}{EF}$,再由已知条件证出BE=DG,得出DF=EF,即可得出结论.
解答 证明:∵DE∥GB,
∴$\frac{AD}{BE}=\frac{AC}{BC}$,$\frac{DG}{DF}=\frac{BE}{EF}$,
∵$\frac{AD}{DG}$=$\frac{AC}{BC}$,
∴$\frac{AD}{BE}=\frac{AD}{DG}$,
∴BE=DG,
∴DF=EF,
∴△DEF是等腰三角形.
点评 本题考查了等腰三角形的判定、平行线分线段成比例定理;熟练掌握平行线分线段成比例定理,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
20.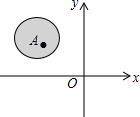 如图,点A在平面直角坐标系中的位置被阴影部分覆盖了,则点A的坐标可能为( )
如图,点A在平面直角坐标系中的位置被阴影部分覆盖了,则点A的坐标可能为( )
 如图,点A在平面直角坐标系中的位置被阴影部分覆盖了,则点A的坐标可能为( )
如图,点A在平面直角坐标系中的位置被阴影部分覆盖了,则点A的坐标可能为( )| A. | (3,2) | B. | (-4,3) | C. | (-2,-3) | D. | (3,-2) |
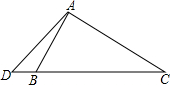 已知,如图,在△ABC中,∠BAC≠90°,∠ABC=2∠C,AD⊥AC,交BC或CB的延长线于D,试说明DC=2AB.
已知,如图,在△ABC中,∠BAC≠90°,∠ABC=2∠C,AD⊥AC,交BC或CB的延长线于D,试说明DC=2AB.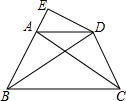 四边形ABCD是等腰梯形,AB=CD,AD∥BC,DE∥CA交BA的延长线于点E,求证:ED•AB=EA•BD.
四边形ABCD是等腰梯形,AB=CD,AD∥BC,DE∥CA交BA的延长线于点E,求证:ED•AB=EA•BD. 如图,直线AB、CD相交于点O,OE⊥CD,若∠1=60°,则∠2=30°.
如图,直线AB、CD相交于点O,OE⊥CD,若∠1=60°,则∠2=30°.