题目内容
5.已知a,b,c是满足$\left\{\begin{array}{l}{4a-5b+2c=0}\\{a+4b-3c=0}\end{array}\right.$,且abc≠0,则a:b:c=1:2:3.分析 根据加减消元法,可得21b-14c=0,根据代入消元法,可得5a-$\frac{2c}{3}$-c=0,根据比的性质,可得答案.
解答 解:$\left\{\begin{array}{l}{4a-5b+2c=0①}\\{a+4b-3c=0②}\end{array}\right.$,
①+②,得
5a-b-c=0 ③,
②×5得
5a+20b-15c=0 ④
21b-14c=0,
b=$\frac{2c}{3}$.
将b=$\frac{2c}{3}$代入③,得
5a-$\frac{2c}{3}$-c=0
解得a=$\frac{c}{3}$,
a:b:c=$\frac{c}{3}$:$\frac{2c}{3}$:c=1:2:3,
故答案为:1:2:3.
点评 本题考查了解三元一次方程组,利用加减消元法、代入消元法得出b=$\frac{2c}{3}$、a=$\frac{c}{3}$是解题关键.

练习册系列答案
相关题目
13.设n是正整数,则10n+1是( )
| A. | n个10相乘所得的积 | B. | 一个(n+1)位的整数 | ||
| C. | 10后面有(n+1)个0的整数 | D. | 一个(n+2)位的整数 |
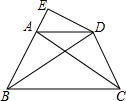 四边形ABCD是等腰梯形,AB=CD,AD∥BC,DE∥CA交BA的延长线于点E,求证:ED•AB=EA•BD.
四边形ABCD是等腰梯形,AB=CD,AD∥BC,DE∥CA交BA的延长线于点E,求证:ED•AB=EA•BD.