题目内容
14.已知ab≠0,且有5a2+1997a+8=0及8b2+1997b+5=0,求$\frac{a}{b}$的值.分析 已知a•b≠1,且有5a2+1997a+8=0及8b2+1997b+5=0,所以a、$\frac{1}{b}$是方程5x2+1997x+8=0的两根,根据根与系数的关系即可求解.
解答 解:由已知5a2+1997a+8=0可得a是方程5x2+1997x+8=0的解,
方程8b2+1997b+5=0,可得$\frac{1}{b}$是方程5x2+1997x+8=0的解,
∴a、$\frac{1}{b}$是方程5x2+1997x+8=0的两根,
由韦达定理可得$\frac{a}{b}$=$\frac{8}{5}$.
点评 此题主要考查了根与系数的关系,得出a、$\frac{1}{b}$是方程5x2+1997x+8=0的两根是解题关键.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
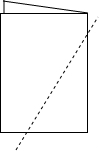 把一张长方形纸对折,任意剪出一个直角边在折线上的直角三角形,把它展开,得到三角形记为△ABC,并将折线的另一端点记为D,如图所示,这是什么特殊三角形?图中有哪些相等的角?有哪些相等的线段?在△ABC中,AD有几种角色?各是什么?
把一张长方形纸对折,任意剪出一个直角边在折线上的直角三角形,把它展开,得到三角形记为△ABC,并将折线的另一端点记为D,如图所示,这是什么特殊三角形?图中有哪些相等的角?有哪些相等的线段?在△ABC中,AD有几种角色?各是什么?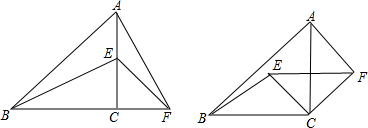
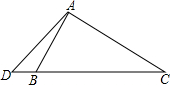 已知,如图,在△ABC中,∠BAC≠90°,∠ABC=2∠C,AD⊥AC,交BC或CB的延长线于D,试说明DC=2AB.
已知,如图,在△ABC中,∠BAC≠90°,∠ABC=2∠C,AD⊥AC,交BC或CB的延长线于D,试说明DC=2AB. 如图,直线AB、CD相交于点O,OE⊥CD,若∠1=60°,则∠2=30°.
如图,直线AB、CD相交于点O,OE⊥CD,若∠1=60°,则∠2=30°.