Question

2．如图，在平面直角坐标系中，等边△OAB的顶点0为坐标原点，B点坐标为（4，0），且△OAB的面积为4$\sqrt{3}$，点P从A点出发沿射线AB运动．点Q从B点出发沿x轴正半轴运动，点P、点Q同时出发，速度均为每秒2个单位长度．运动时间为t秒，过点P作PH⊥x轴于点H．
（1）求A点的坐标；
（2）当点P在线段AB上运动时，用含t的式子表示线段BQ的长度．
（3）在点P0、点Q的运动过程，当∠PQB=30°时，求点P、点Q运动时间t的值．

Answer 1

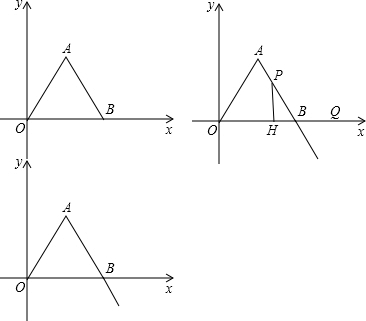
分析 （1）如图1，过A作AD⊥OB于D，由△AOB是等边三角形，得到OD=$\frac{1}{2}$OB=2，根据△OAB的面积为4$\sqrt{3}$，求出AD=2$\sqrt{3}$，于是得到结果；
（2）根据路程=速度×时间即可得到BQ=2t；
（3）如图2，当点P在线段AB上时，由△ABO是等边三角形，得到∠ABO=60°，推出△PBQ是等腰三角形，根据等腰三角形的性质列方程即可得到结论；当P在射线AB上时，如图3，连接PQ，由△ABO是等边三角形，得到∠PBQ=∠ABO=60°，推出△PQB是直角三角形，由直角三角形的性质列方程即可得到结论．

解答 解：（1）如图1，过A作AD⊥OB于D，
∵B点坐标为（4，0），
∴OB=4，
∵△AOB是等边三角形，
∴OD=$\frac{1}{2}$OB=2，
∵△OAB的面积为4$\sqrt{3}$，
∴$\frac{1}{2}×OB•AD$=4$\sqrt{3}$，
∴AD=2$\sqrt{3}$，
∴A点的坐标为：（2.2$\sqrt{3}$）；

（2）BQ=2t；

（3）如图2，当点P在线段AB上时，
∵△ABO是等边三角形，
∴∠ABO=60°，
∵∠PQB=30°，
∴∠BPQ=30°，
∴∠PQB=∠BPQ，
∴PB=BQ，
即4-2t=2t，
∴t=1，
当P在射线AB上时，如图3，连接PQ，
∵△ABO是等边三角形，
∴∠ABO=60°，
∴∠PBQ=∠ABO=60°，
∵∠PQB=30°，
∴∠BPQ=90°，
∴BQ=2PB，
即2t=2（2t-4），
∴t=4，
∴当t=1或4时，∠PQB=30°．

点评 本题考查了等边三角形的性质，坐标与图形的性质，直角三角形的性质，正确的理解题意是解题的关键．