题目内容
1.已知A(x1,2015),B(x2,2015)是二次函数y=ax2+bx+3(a≠b)的图象上两点,则当x=x1+x2时,二次函数的值是( )| A. | -$\frac{{b}^{2}}{4a}$+3 | B. | $\frac{2{b}^{2}}{a}$+3 | C. | 2015 | D. | 3 |
分析 根据题意得出x=x1+x2=-$\frac{b}{a}$,代入函数的解析式即可求得二次函数的值.
解答 解:∵A(x1,2015),B(x2,2015)是二次函数y=ax2+bx+3(a≠b)的图象上两点,
∴x1、x2是方程ax2+bx+3=2015的两个根,
∴x1+x2=-$\frac{b}{a}$,
∴当x=x1+x2时,二次函数y=ax2+bx+3=a(-$\frac{b}{a}$)2+b(-$\frac{b}{a}$)+3=$\frac{{b}^{2}}{a}$-$\frac{{b}^{2}}{a}$+3=3.
故选D.
点评 本题考查了一元二次方程根与系数的关系以及二次函数图象上点的坐标特征,图象上的点符合解析式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.设n是正整数,则10n+1是( )
| A. | n个10相乘所得的积 | B. | 一个(n+1)位的整数 | ||
| C. | 10后面有(n+1)个0的整数 | D. | 一个(n+2)位的整数 |
 如图,在一圆柱的下底边沿A处有一只蚂蚁,它不走直线而是绕着圆柱侧面,找出蚂蚁到B处的最短路径.
如图,在一圆柱的下底边沿A处有一只蚂蚁,它不走直线而是绕着圆柱侧面,找出蚂蚁到B处的最短路径.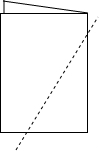 把一张长方形纸对折,任意剪出一个直角边在折线上的直角三角形,把它展开,得到三角形记为△ABC,并将折线的另一端点记为D,如图所示,这是什么特殊三角形?图中有哪些相等的角?有哪些相等的线段?在△ABC中,AD有几种角色?各是什么?
把一张长方形纸对折,任意剪出一个直角边在折线上的直角三角形,把它展开,得到三角形记为△ABC,并将折线的另一端点记为D,如图所示,这是什么特殊三角形?图中有哪些相等的角?有哪些相等的线段?在△ABC中,AD有几种角色?各是什么?