题目内容
17.一张长方形的餐桌可以坐6个人,按照下图的方式摆放餐桌和椅子:
(1)n张餐桌拼放在一起可坐(2n+4)个人(用含n的式子表示);
(2)一家酒楼,按上图的方式拼桌,要使拼成的一张大餐桌刚好能坐160人,请问需几张餐桌拼成一张大餐桌?
分析 (1)从餐桌和椅子的摆放方式,可总结出每多放一张桌子,就多坐两个人,由此得出n张餐桌拼放在一起可坐(2n+4)个人;
(2)根据拼成的一张大餐桌刚好能坐160人列出方程,求解即可.
解答 解:(1)由图可知,1张餐桌可坐6个人,6=2×1+4;
2张餐桌拼放在一起可坐8个人,8=2×2+4;
3张餐桌拼放在一起可坐10个人,10=2×3+4;
即每多放一张桌子,就多坐两个人,
所以n张餐桌拼放在一起可坐(2n+4)个人;
(2)设需n张餐桌拼成一张大餐桌,得2n+4=160,
解得n=78.
答:需78张餐桌拼成一张大餐桌.
故答案为(2n+4).
点评 本题考查了一元一次方程的应用,以及图形的变化类问题,关键是通过归纳与总结,得到n张餐桌拼放在一起可坐的人数.

练习册系列答案
相关题目
7.不解方程,判断方程2x2-4x-1=0的根的情况( )
| A. | 没有实数根 | B. | 有两个相等实数根 | ||
| C. | 有两个不相等实数根 | D. | 无法确定 |
8.下列说法中正确的个数是( )
①一个数与它的相反数的商为-1;
②两个有理数之和大于其中任意一个加数;
③若两数之和为正数,则这两个数一定都是正数;
④若m<0<n,则mn<n-m.
①一个数与它的相反数的商为-1;
②两个有理数之和大于其中任意一个加数;
③若两数之和为正数,则这两个数一定都是正数;
④若m<0<n,则mn<n-m.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
2.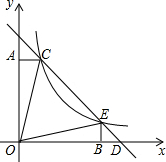 如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支交于C(1,4),E两点,CA⊥y轴于点A,EB⊥x轴于点B,则以下结论:①k的值为4;②△BED是等腰直角三角形;③S△ACD=S△BED;④S△CBD=15;⑤点D的坐标为(5,0).其中正确的是( )
如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支交于C(1,4),E两点,CA⊥y轴于点A,EB⊥x轴于点B,则以下结论:①k的值为4;②△BED是等腰直角三角形;③S△ACD=S△BED;④S△CBD=15;⑤点D的坐标为(5,0).其中正确的是( )
 如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支交于C(1,4),E两点,CA⊥y轴于点A,EB⊥x轴于点B,则以下结论:①k的值为4;②△BED是等腰直角三角形;③S△ACD=S△BED;④S△CBD=15;⑤点D的坐标为(5,0).其中正确的是( )
如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支交于C(1,4),E两点,CA⊥y轴于点A,EB⊥x轴于点B,则以下结论:①k的值为4;②△BED是等腰直角三角形;③S△ACD=S△BED;④S△CBD=15;⑤点D的坐标为(5,0).其中正确的是( )| A. | ①②③ | B. | ①②③④ | C. | ②③④⑤ | D. | ①②⑤ |
7.下列各式中,正确的是( )
| A. | 一个图形平移后,形状和大小都改变 | |
| B. | 一个图形平移后,形状和大小都不变 | |
| C. | 一个图形平移后,形状改变但大小不变 | |
| D. | 一个图形平移后,形状不变但大小改变 |