题目内容
2.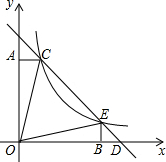 如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支交于C(1,4),E两点,CA⊥y轴于点A,EB⊥x轴于点B,则以下结论:①k的值为4;②△BED是等腰直角三角形;③S△ACD=S△BED;④S△CBD=15;⑤点D的坐标为(5,0).其中正确的是( )
如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支交于C(1,4),E两点,CA⊥y轴于点A,EB⊥x轴于点B,则以下结论:①k的值为4;②△BED是等腰直角三角形;③S△ACD=S△BED;④S△CBD=15;⑤点D的坐标为(5,0).其中正确的是( )| A. | ①②③ | B. | ①②③④ | C. | ②③④⑤ | D. | ①②⑤ |
分析 ①只需把点C的坐标代入两个函数的解析式,就可得到k和b的值;②易证OD=OF,从而可得∠ODF=45°,即可证到△BED是等腰直角三角形;③只需求出点E的坐标,就可求出△ACD和△BED的面积;④只需根据点C、B、D的坐标就可求出△CBD的面积;⑤把yD=0代入直线的解析式,就可解决问题.
解答 解:①∵直线y=-x+b与反比例函数y=$\frac{k}{x}$(k≠0)的图象的一支交于C(1,4),
∴4=-1+b,k=xy=1×4=4,故①正确;
②∵点D、F分别是直线y=-x+5与x轴、y轴的交点,
∴点D的坐标为(5,0),点F的坐标为(0,5),
∴OD=OF=5.
∵∠DOF=90°,
∴∠ODF=45°.
∵EB⊥x轴,
∴△BED是等腰直角三角形,故②正确;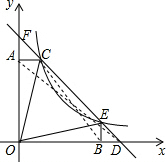
③解方程组$\left\{\begin{array}{l}{y=-x+5}\\{y=\frac{4}{x}}\end{array}\right.$,得
$\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$或$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$,
∴E的坐标为(4,1),
∵AC=1,OA=4,OD=5,OB=4,
∴BD=1,
∴S△ACD=$\frac{1}{2}$AC•OA=$\frac{1}{2}$×1×4=2,S△BED=$\frac{1}{2}$BD•BE=$\frac{1}{2}$×1×1=$\frac{1}{2}$,
故③错误;
④S△CBD=$\frac{1}{2}$BD•OA=$\frac{1}{2}$×1×4=2,故④错误;
⑤∵点D是直线y=-x+5与x轴的交点,
∴点D的坐标为(5,0),故⑤正确.
故选D.
点评 本题主要考查了一次函数与反比例函数的交点、直线上点的坐标特征、等腰直角三角形的判定与性质、三角形的面积公式等知识,求出点D、E、F的坐标是解决本题的关键.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案| A. | 0.256×10-14 | B. | 2.56×10-15 | C. | 0.256×10-15 | D. | 256×10-17 |
| A. |  | B. |  | C. |  | D. |  |
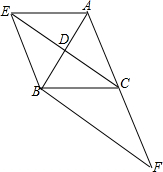 已知,如图,在三角形ABC中,CD是中线,过点A作平行线BC的平行线,交CD的延长线于点E,连接EB.
已知,如图,在三角形ABC中,CD是中线,过点A作平行线BC的平行线,交CD的延长线于点E,连接EB.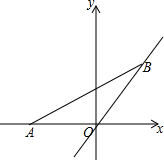 如图,点A的坐标为(-1,0),点B(a,a),当线段AB最短时,点B的坐标为(-$\frac{1}{2}$,-$\frac{1}{2}$).
如图,点A的坐标为(-1,0),点B(a,a),当线段AB最短时,点B的坐标为(-$\frac{1}{2}$,-$\frac{1}{2}$).