题目内容
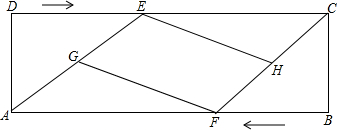
2.如图,Rt△EFG中,∠E=90°,EG=$\frac{15}{4}$,sinF=$\frac{3}{5}$,?ABCD中,AB=7,AC=10,H为AB边上一点,AH=5,AC∥EF,斜边FG与边AB在同一直线上,Rt△EFG从图①(点G与点A重合)的位置出发,以每秒1个单位的速度沿射线AB方向匀速移动,当F与H重合时,停止运动.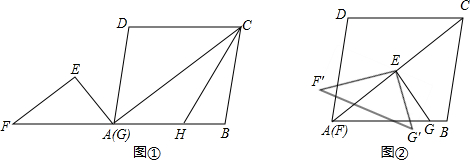
(1)求BC的长;
(2)设△EFG在运动中与△ACH重叠的部分面积为S,请直接写出S与运动时间t(秒)之间的函数关系式,并写出t的取值范围;
(3)如图②,当E在AC上时,将△FGE绕点E顺时针旋转a°(0<a<180),记旋转中的△FGE为△F′G′E,在旋转过程中,设直线F′G′与直线AC交于M,与直线AB交于点N,是否存在这样的M、N两点,使△AMN为等腰三角形?若存在,求出此时EM的值;若不存在,请说明理由.
分析 (1)作CI⊥直线AB,利用锐角三角函数的意义与勾股定理求得答案即可;
(2)分类探讨:在0≤t≤$\frac{45}{4}$的范围内进一步分段,利用三角形的面积的和与差以及计算方法得出答案即可;
(3)分三种情况探讨:AM=AN.MA=MN,NA=NM利用勾股定理探讨得出答案即可.
解答 解:(1)如图,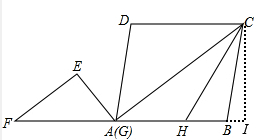
过C作CI⊥直线AB,
∵AC∥EF,
∴∠CAB=∠F,
在Rt△ACI中,
sin∠CAB=sinF=$\frac{CI}{AC}$=$\frac{3}{5}$,
∴CI=$\frac{3}{5}$×10=6,
在Rt△ACI中,
AI=$\sqrt{A{C}^{2}-I{C}^{2}}$=8,
∴BI=AI-7=1
在Rt△BCI中,
BC=$\sqrt{C{I}^{2}+B{I}^{2}}$=$\sqrt{37}$;
(2)S=$\left\{\begin{array}{l}{\frac{6}{25}{t}^{2}(0≤t≤5)}\\{-\frac{4}{25}{t}^{2}+4t-10(5<t≤\frac{25}{4})}\\{-\frac{2}{5}{t}^{2}+4t-\frac{5}{8}(\frac{25}{4}<t≤\frac{35}{4})}\\{\frac{3}{5}{t}^{2}-\frac{27}{2}t+\frac{1215}{16}(\frac{35}{4}<t≤\frac{45}{4})}\end{array}\right.$
(3)过E作EK⊥AB
如图1,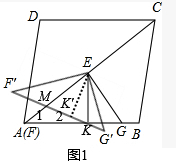
当MA=MN时∠1=∠2,
又∵∠F′=∠1
∴∠3=∠1=∠F′,
∴MF′=ME,
在Rt△EK′M中,
EM2=(4-EM)2+EK′2,
∴EM=$\frac{25}{8}$;
如图2,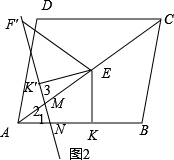
当AM=AN时,
∵∠EFK=∠F′,
∴∠1=∠2=∠3=∠F′EM,
∴F′M=F′E=5,
∴K′M=F′M-K′M=5-4=1,
∴Rt△EK′M中,
EM2=EK′2+K′M2,
∴EM=$\sqrt{10}$;
如图3: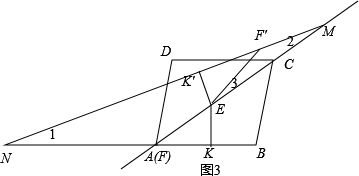
当AM=AN时∠1=∠2,
∵∠EFK=∠1+∠2=∠K′F′E=∠3+∠2
∴∠3=∠2,F′E=F′M=5,
∴Rt△EK′M中
ME2=K′M2+K′E2,
EM=3$\sqrt{10}$,
如图4: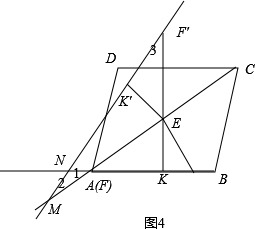
当NM=NA时,
∠1=∠2=∠EFK=∠3
∴F′E=ME,
∴M与F重合,
∴EM=$\frac{25}{8}$,$\sqrt{10}$,3$\sqrt{10}$.
点评 此题考查四边形的综合题,综合运用锐角三角函数的意义,勾股定理,等腰三角形的性质,旋转的性质,正确作出辅助线是解决问题的关键.

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案| A. | a<0 | |
| B. | b2-4ac的值可能为0 | |
| C. | 方程ax2+bx+c=0必有一根x0满足x1<x0<x2 | |
| D. | y1<y2 |
| A. | 3 | B. | -2 | C. | -3 | D. | 1 |
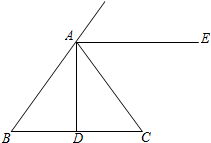 如图,在△ABC中,AB=AC,D为BC边的中点,AE∥BC.
如图,在△ABC中,AB=AC,D为BC边的中点,AE∥BC.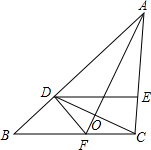 已知:如图,在△ABC中,D是AB上一点,且AD=AC,∠DAO=∠CAO,DE∥BC.求证:CD平分∠EDF.
已知:如图,在△ABC中,D是AB上一点,且AD=AC,∠DAO=∠CAO,DE∥BC.求证:CD平分∠EDF.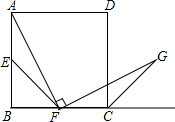 如图,在正方形ABCD中,点E、F分别是边AB、BC的中点,∠AFG=90°,且FG交正方形的外角∠DCP的平分线CG于点G.
如图,在正方形ABCD中,点E、F分别是边AB、BC的中点,∠AFG=90°,且FG交正方形的外角∠DCP的平分线CG于点G.