题目内容
7．
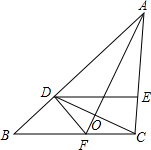已知：如图，在△ABC中，D是AB上一点，且AD=AC，∠DAO=∠CAO，DE∥BC．求证：CD平分∠EDF．
分析 由等腰三角形“三线合一”的性质，得到线段的垂直平分线，由线段的垂直平分线的性质得到等腰三角形，根据平行线的性质得到内错角相等，由等量代换得到结论．
解答 证明：∵AD=AC，∠DAO=∠CAO，
∴AF垂直平分CD，
∴CF=DF，
∴∠FDC=∠FCD，
∵DE∥BC，
∴∠EDC=∠DCF，
∴∠EDC=FDC，
∴CD平分∠EDF．
点评 本题考查了等腰三角形的性质“三线合一”，线段垂直平分线的性质，平行线的性质，掌握线段垂直平分线的性质是解决本题的关键．
练习册系列答案
相关题目
如图，已知平行四边形OABC中，O（0，0），A（-3，-4），B（1，2），求点C的坐标．
点E，F，G，H分别是四边形ABCD的边AB，BC，CD，DA的中点．