题目内容
14.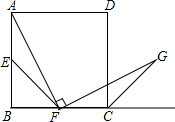 如图,在正方形ABCD中,点E、F分别是边AB、BC的中点,∠AFG=90°,且FG交正方形的外角∠DCP的平分线CG于点G.
如图,在正方形ABCD中,点E、F分别是边AB、BC的中点,∠AFG=90°,且FG交正方形的外角∠DCP的平分线CG于点G.(1)求证:∠BAF=∠CFG;
(2)求证:△AEF≌△FCG;
(3)连接DE、DG,判定四边形DEFG是怎样的四边形?并说明理由.
分析 (1)由于∠AFG是直角,则∠BAF,∠CFG同为∠AFB的余角,由此得证;
(2)根据正方形的性质,易证得AE=FC,∠AEF=∠GCF=135°;再加上(1)得出的相等角,可由ASA判定两个三角形全等;
(3)由(2)证得△AEF≌△FCG,得到AF=FG,由△AED≌△ABF,得到DE=AF,∠1=∠3,根据互余角的关系得到两边平行的条件,然后根据一组对边平行且相等得到结论
解答 解:(1)证明:∵∠AFG=90°,
∴∠GFC+∠AFB=90°,
在Rt△ABF中,∠AFB+∠BAF=90°,
∴∠BAF=∠GFC;
(2)证明:∵E,F分别是正方形ABCD的边AB,BC的中点,
∴AE=BE=BF=CF,
∴∠AEB=135°,
∵CG是正方形的外角∠DCP的平分线,
∴∠FCG=135°,
在△AEF与△FCG中,
$\left\{\begin{array}{l}{∠EAF=∠CFG}\\{AE=CF}\\{∠AEF=∠FCG}\end{array}\right.$,
∴△AEF≌△FCG;
(3) 由(2)证得△AEF≌△FCG,
由(2)证得△AEF≌△FCG,
∴AF=FG,
在△AED与△ABF中,
$\left\{\begin{array}{l}{AD=AB}\\{∠DAB=∠B}\\{AE=BF}\end{array}\right.$,
∴△AED≌△ABF,
∴DE=AF,∠1=∠3,
∴DE=FG,
∵∠2+∠3=90°,
∴∠1+∠2=90°,
∴DE⊥AF,
∴DE∥GF,
∴四边形DEFG是平行四边形.
点评 此题主要考查了正方形的性质、全等三角形的判定和性质、等腰直角三角形的判定和性质等;综合性较强,难度适

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
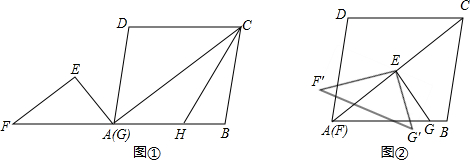
 如图,在△ABC中,AB=8cm,BC=16cm,动点P从点A开始沿AB边运动,速度为2cm/s;动点Q从点B开始沿BC边运动,速度为4cm/s;如果P、Q两动点同时运动,那么何时△QBP与△ABC相似?
如图,在△ABC中,AB=8cm,BC=16cm,动点P从点A开始沿AB边运动,速度为2cm/s;动点Q从点B开始沿BC边运动,速度为4cm/s;如果P、Q两动点同时运动,那么何时△QBP与△ABC相似? 点E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点.
点E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点.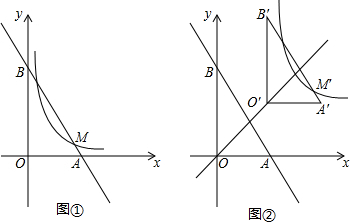
 如图,在△ABC中,AB=AC,点D在AC上,AD=2CD,△ABC的周长为16,△ABD的周长比△CBD大4,求BC的长.
如图,在△ABC中,AB=AC,点D在AC上,AD=2CD,△ABC的周长为16,△ABD的周长比△CBD大4,求BC的长.