题目内容
10.若△ABC∽△DEF,且△ABC与△DEF的相似比为1:2,则△ABC与△DEF的面积比为1:4.分析 根据相似三角形面积的比等于相似比的平方解答即可.
解答 解:∵△ABC∽△DEF,且△ABC与△DEF的相似比为1:2,
∴△ABC与△DEF的面积比为1:4,
故答案为:1:4.
点评 本题考查的是相似三角形的性质,掌握相似三角形面积的比等于相似比的平方是解题的关键.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
20.已知抛物线y1=a(x-m)2+k与y2=a(x+m)2+k(m≠0)关于y轴对称,我们称y1与y2互为“和谐抛物线”.请写出抛物线y=-4x2+6x+7的“和谐抛物线”y=-4x2-6x+7.
19.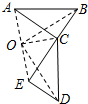 如图,△ABC绕着点O按顺时针方向旋转90°后到达了△CDE的位置,下列说法中不正确的是( )
如图,△ABC绕着点O按顺时针方向旋转90°后到达了△CDE的位置,下列说法中不正确的是( )
 如图,△ABC绕着点O按顺时针方向旋转90°后到达了△CDE的位置,下列说法中不正确的是( )
如图,△ABC绕着点O按顺时针方向旋转90°后到达了△CDE的位置,下列说法中不正确的是( )| A. | 线段AB与线段CD互相垂直 | B. | 线段AC与线段CE互相垂直 | ||
| C. | 点A与点E是两个三角形的对应点 | D. | 线段BC与线段DE互相垂直 |
 如图,长2.5m的梯子靠在墙上,梯子的底部离墙的底端1.5m,求梯子的顶端与地面的距离h;由于地面有水,梯子底部向右滑动0.9m,则梯子上端下滑多少m?
如图,长2.5m的梯子靠在墙上,梯子的底部离墙的底端1.5m,求梯子的顶端与地面的距离h;由于地面有水,梯子底部向右滑动0.9m,则梯子上端下滑多少m? 如图,直线AB、CD相交于点O,已知∠AOC=75°,OE把∠BOD分成两个角,且∠BOE:∠EOD=2:3.
如图,直线AB、CD相交于点O,已知∠AOC=75°,OE把∠BOD分成两个角,且∠BOE:∠EOD=2:3.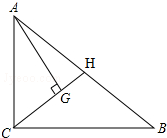 如图,在△ABC中,∠ACB=90°,点G是△ABC的重心,且AG⊥CG,CG的延长
如图,在△ABC中,∠ACB=90°,点G是△ABC的重心,且AG⊥CG,CG的延长 建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条参照线,使垒的每一层砖在一条直线上.这样做的依据是:两点确定一条直线.
建筑工人在砌墙时,经常用细线绳在墙的两端之间拉一条参照线,使垒的每一层砖在一条直线上.这样做的依据是:两点确定一条直线.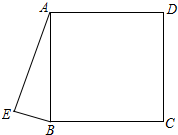 如图,正方形ABCD和直角△ABE,∠AEB=90°,将△ABE绕点O旋转180°得到△CDF.
如图,正方形ABCD和直角△ABE,∠AEB=90°,将△ABE绕点O旋转180°得到△CDF.