题目内容
5.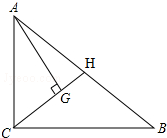 如图,在△ABC中,∠ACB=90°,点G是△ABC的重心,且AG⊥CG,CG的延长
如图,在△ABC中,∠ACB=90°,点G是△ABC的重心,且AG⊥CG,CG的延长线交AB于H.
(1)求证:△CAG∽△ABC;
(2)求S△AGH:S△ABC的值.
分析 (1)证明:CG交AB于D,如图,设GD=a,根据重心的性质得CG=2DG=2a,根据重心的定义得CD为AB边上的中线,接着根据直角三角形斜边上的中线性质得到CD=AD=BD=3a,则∠1=∠3,再利用等角的余角相等得∠1=∠3,所以∠B=∠3,加上∠ACB=∠AGC=90°,于是根据相似三角形的判定方法得到△CAG∽△ABC;
(2)由点G是△ABC的重心,得到CG=2HG,于是得到HG=$\frac{1}{3}$CH,求得S△AHG=$\frac{1}{3}$S△ACH,根据CH为AB边上的中线,于是得到S△ACH=$\frac{1}{2}$S△ABC,推出S△AHG=$\frac{1}{3}×\frac{1}{2}$S△ABC,即可得到结论.
解答 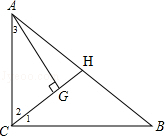 (1)证明:如图,设GH=a,
(1)证明:如图,设GH=a,
∵点G是△ABC的重心,
∴CG=2HG=2a,CH为AB边上的中线,
∴CH=AH=BH=3a,
∴∠1=∠3,
∵AG⊥CG,
∴∠2+∠3=90°,
而∠1+∠2=90°,
∴∠1=∠3,
∴∠B=∠3,
而∠ACB=∠AGC=90°,
∴△CAG∽△ABC;
(2)∵点G是△ABC的重心,
∴CG=2HG,
∴HG=$\frac{1}{3}$CH,
∴S△AHG=$\frac{1}{3}$S△ACH,
∵CH为AB边上的中线,
∴S△ACH=$\frac{1}{2}$S△ABC,
∴S△AHG=$\frac{1}{3}×\frac{1}{2}$S△ABC,
∴S△AGH:S△ABC=1:6.
点评 本题考查了三角形的重心:三角形的重心是三角形三边中线的交点;重心到顶点的距离与重心到对边中点的距离之比为2:1.也考查相似三角形的判定与性质.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目