题目内容
20.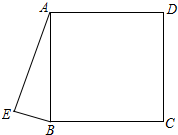 如图,正方形ABCD和直角△ABE,∠AEB=90°,将△ABE绕点O旋转180°得到△CDF.
如图,正方形ABCD和直角△ABE,∠AEB=90°,将△ABE绕点O旋转180°得到△CDF.(1)在图中画出点O和△CDF,并简要说明作图过程;
(2)若AE=12,AB=13,求EF的长.
分析 (1)利用旋转的性质分别得出对应点位置进而得出答案;
(2)首先过点O作OG⊥OE与EB的延长线交于点G,利用正方形的性质结合全等三角形的判定方法得出△EAO≌△GBO(ASA),得出△GEO为等腰直角三角形,进而得出答案.
解答 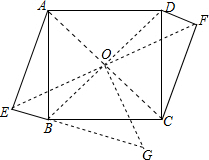 解:(1)如图所示:连接AC,BD,交于点O.连接EO并延长到点F,使OF=OE,连接DF,CF,
解:(1)如图所示:连接AC,BD,交于点O.连接EO并延长到点F,使OF=OE,连接DF,CF,
(2)如图所示:过点O作OG⊥OE与EB的延长线交于点G,
∵四边形ABCD为正方形
∴OA=OB,∠AOB=∠EOG=90°
∴∠AOE=∠BOG
在四边形AEBO中
∠AEB=∠AOB=90°
∴∠EAO+∠EBO=180°=∠EBO+∠GBO
∴∠GBO=∠EAO,
∴在△EAO和△GBO中,
∵$\left\{\begin{array}{l}∠EAO=∠GBO\\ OA=OB\\∠AOE=∠BOG\end{array}\right.$
∴△EAO≌△GBO(ASA),
∴AE=BG,OE=OG.
∴△GEO为等腰直角三角形,
∴OE=$\frac{\sqrt{2}}{2}$EG=$\frac{\sqrt{2}}{2}$(EB+BG)
=$\frac{\sqrt{2}}{2}$(EB+AE)
=$\frac{{17\sqrt{2}}}{2}$
∴EF=$17\sqrt{2}$.
点评 此题主要考查了旋转变换以及全等三角形的判定与性质以及等腰直角三角形的性质等知识,得出△GEO为等腰直角三角形是解题关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
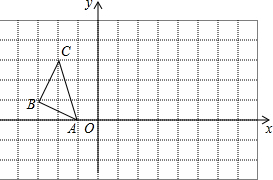 如图,△ABC的三个顶点都在方格纸的格点上,其中点A的坐标是(-1,0).画出将△ABC绕点A顺时针旋转90°后的图形△A′B′C′,并写出点C′的坐标.
如图,△ABC的三个顶点都在方格纸的格点上,其中点A的坐标是(-1,0).画出将△ABC绕点A顺时针旋转90°后的图形△A′B′C′,并写出点C′的坐标. 动手画一画,请把下图补成以A为对称中心的中心对称图形.
动手画一画,请把下图补成以A为对称中心的中心对称图形.