题目内容
3．有一块长为70cm、宽为50cm的矩形木板，要把它改拼成一块正方形木板，能改拼成最大边长是多少的正方形木板？（精确到0.01cm）分析 根据长方形的面积=改拼成的正方形纸板面积，列方程求得正方形的边长，取近似值即可得答案．
解答 解：设改拼成的正方形纸板的边长为xcm，
则x2=50×70，
解得：x=-5$\sqrt{14}$（舍）或x=5$\sqrt{14}$≈18.71（cm），
答：能改拼成最大边长是18.71cm的正方形木板．
点评 本题主要考查图形的剪拼、近似数和有效数字、解一元二次方程的能力，根据图形剪拼前后面积不变列出方程式解题的关键．
练习册系列答案
相关题目
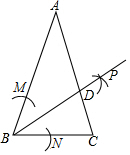△ABC中，AB=AC，∠ABC=72°，以B为圆心，以任意长为半径画弧，分别交BA、BC于M、N，再分别以M、N为圆心，以大于$\frac{1}{2}$MN为半径画弧，两弧交于点P，射线BP交AC于点D，则图中与BC相等的线段有（ ）
如图所示，已知∠1+∠2=180°，∠B=∠D，AD平分∠EAC，那么CB平分∠ACF吗？为什么？
为了测量校园内旗杆的高度，小强先将升旗的绳子拉直到旗杆底端，并在与旗杆低端齐平的绳子处做好标记，测得剩余绳子的长度为0.5米，然后将绳子低端拉至离旗杆底端3.5米处（绳子被拉直且低端恰好与地面接触）．请你算出旗杆的高度．
如图是一个直角梯形，上底的长是下底长的$\frac{1}{4}$，阴影部分的面积是整个直角梯形面积的80%．
如图，矩形BCDE的各边分别平行于x轴或y轴，物体甲和物体乙分别由点A（2，0）同时出发，沿矩形BCDE的边作环绕运动，物体甲按逆时针方向以1个单位/秒匀速运动，物体乙按顺时针方向以2个单位/秒匀速运动，则两个物体运动后的第2016次相遇地点的坐标是（2，0）．