题目内容
16.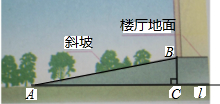 如图,一座大楼前的残疾人通道是斜坡,用AB表示,沿着通道走3.2米进入楼厅,楼厅比楼外的地面高0.4米,求残疾人通道的坡度与坡角(角度精确到1′,其他近似数值精确到0.01).
如图,一座大楼前的残疾人通道是斜坡,用AB表示,沿着通道走3.2米进入楼厅,楼厅比楼外的地面高0.4米,求残疾人通道的坡度与坡角(角度精确到1′,其他近似数值精确到0.01).
分析 根据勾股定理可以求得AC的长度,然后由余切函数的定义来求残疾人通道的坡度与坡角.
解答 解:由题意知,∠ACB=90°,AB=3.2米,BC=0.4米.
由勾股定理得到:AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{3.{2}^{2}-0.{4}^{2}}$≈3.1749.
则i=$\frac{BC}{AC}$=$\frac{0.4}{3.1749}$≈1:7.938.
因为tanA=$\frac{BC}{AC}$=$\frac{0.4}{3.1749}$≈0.12599,
所以A=7°11′
点评 本题考查了解直角三角形的应用--坡度坡脚问题.坡度是坡面的铅直高度h和水平宽度l的比,又叫做坡比,它是一个比值,反映了斜坡的陡峭程度,一般用i表示,常写成i=1:m的形式.(2)把坡面与水平面的夹角α叫做坡角,坡度i与坡角α之间的关系为:i=$\frac{h}{l}$=tanα.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.(1)如表,方程1、方程2、方程3…是按照一定的规律排列的一列方程,解方程1,并将它的解填在表中的空白处.
(2)方程$\frac{x}{10}$-(x-a)=1的解是x=$\frac{70}{9}$,求a的值.该方程是否是(1)中所给出的一列方程中的一个方程?如果是,它是第几个方程?
| 序号 | 方程 | 方程的解 |
| 1 | $\frac{x}{4}$-(x-2)=1 | x=$\frac{4}{3}$ |
| 2 | $\frac{x}{5}$-(x-3)=1 | x=$\frac{10}{4}$ |
| 3 | $\frac{x}{6}$-(x-4)=1 | x=$\frac{18}{5}$ |
| … | … | … |
 如图,已知AB=AC,∠APC=60°
如图,已知AB=AC,∠APC=60° 如图,在Rt△ABC中,∠A,∠B,∠C的对边分别是a,b,c.证明:sin2A+cos2A=1.
如图,在Rt△ABC中,∠A,∠B,∠C的对边分别是a,b,c.证明:sin2A+cos2A=1.