题目内容
8. 如图,在Rt△ABC中,∠A,∠B,∠C的对边分别是a,b,c.证明:sin2A+cos2A=1.
如图,在Rt△ABC中,∠A,∠B,∠C的对边分别是a,b,c.证明:sin2A+cos2A=1.
分析 根据勾股定理,可得a、b、c的关系,根据锐角的正弦为对边比斜边,余弦为邻边比斜边,可得答案.
解答 证明:∵在Rt△ABC中,∠A,∠B,∠C的对边分别是a,b,c,
∴a2+b2=c2.
∵sinA=$\frac{a}{c}$,cosA=$\frac{b}{c}$,
∴sin2A+cos2A=$\frac{{a}^{2}}{{c}^{2}}$+$\frac{{b}^{2}}{{c}^{2}}$=1.
点评 本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.下列化去根号内分母的变形中,正确的是( )
| A. | $\sqrt{3\frac{1}{4}}$=2$\sqrt{13}$ | B. | $\sqrt{\frac{2m}{3n}}$=3n$\sqrt{6mn}$ | ||
| C. | $\sqrt{\frac{a}{{b}^{2}}+\frac{b}{{a}^{2}}}$=($\frac{1}{a}$+$\frac{1}{b}$)$\sqrt{a+b}$ | D. | $\sqrt{\frac{2{x}^{2}}{27(x-1)^{2}}}$=$\frac{x}{9(x-1)}$$\sqrt{6}$(x>1) |
20.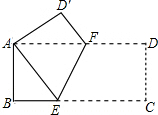 如图,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A重合,则AF的长为( )
如图,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A重合,则AF的长为( )
 如图,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A重合,则AF的长为( )
如图,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A重合,则AF的长为( )| A. | 4$\sqrt{5}$ | B. | 8 | C. | 6 | D. | 10 |
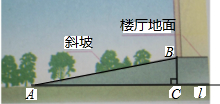 如图,一座大楼前的残疾人通道是斜坡,用AB表示,沿着通道走3.2米进入楼厅,楼厅比楼外的地面高0.4米,求残疾人通道的坡度与坡角(角度精确到1′,其他近似数值精确到0.01).
如图,一座大楼前的残疾人通道是斜坡,用AB表示,沿着通道走3.2米进入楼厅,楼厅比楼外的地面高0.4米,求残疾人通道的坡度与坡角(角度精确到1′,其他近似数值精确到0.01).