题目内容
19.因为$\frac{1}{1×2}$=1-$\frac{1}{2}$,$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$,…,$\frac{1}{19×20}$=$\frac{1}{19}$-$\frac{1}{20}$,所以$\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{19×20}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{19}$-$\frac{1}{20}$=1-$\frac{1}{20}$=$\frac{19}{20}$.
解答下列问题:
(1)在和式$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…中,第九项是$\frac{1}{9×10}$;第n项是$\frac{1}{n(n+1)}$.
(2)解方程$\frac{1}{(x+1)(x+2)}$+$\frac{1}{(x+2)(x+3)}$+…+$\frac{1}{(x+2001)(x+2002)}$=1-$\frac{2}{2x+4004}$.
分析 (1)归纳总结得到第九项,确定出第n项即可;
(2)方程利用拆项法变形,计算即可求出解.
解答 解:(1)第九项为$\frac{1}{9×10}$;第n项是$\frac{1}{n(n+1)}$;
(2)方程整理得:$\frac{1}{x+1}$-$\frac{1}{x+2}$+$\frac{1}{x+2}$-$\frac{1}{x+3}$+…+$\frac{1}{x+2001}$-$\frac{1}{x+2002}$=1-$\frac{1}{x+2002}$,
整理得:$\frac{1}{x+1}$-$\frac{1}{x+2002}$=1-$\frac{1}{x+2002}$,即$\frac{1}{x+1}$=1,
解得:x=0,
经检验x=0是分式方程的解.
故答案为:(1)$\frac{1}{9×10}$;$\frac{1}{n(n+1)}$
点评 此题考查了解分式方程,以及分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.在下列实数中,无理数是( )
| A. | 0.010010001 | B. | $\frac{1}{4}$ | C. | $\sqrt{5}$ | D. | 6 |
11.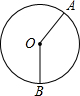 如图,圆中两条半径把圆分成面积为4:5的两个扇形,则两个扇形的圆心角的度数为( )
如图,圆中两条半径把圆分成面积为4:5的两个扇形,则两个扇形的圆心角的度数为( )
 如图,圆中两条半径把圆分成面积为4:5的两个扇形,则两个扇形的圆心角的度数为( )
如图,圆中两条半径把圆分成面积为4:5的两个扇形,则两个扇形的圆心角的度数为( )| A. | 40°和50° | B. | 80°和100° | C. | 120°和150° | D. | 160°和200° |

 一个正方体的表面展开图如图所示,则原正方体中的“★”所在面的对面所标的字是田.
一个正方体的表面展开图如图所示,则原正方体中的“★”所在面的对面所标的字是田.