题目内容
8．先化简，再求值：$\frac{{b}^{2}{-a}^{2}}{a}$÷（a-$\frac{2ab{-b}^{2}}{a}$），其中a=7，b=6．分析 根据分式的减法和除法可以化简题目中的式子，然后将a、b的值代入化简后的式子即可解答本题．
解答 解：$\frac{{b}^{2}{-a}^{2}}{a}$÷（a-$\frac{2ab{-b}^{2}}{a}$）
=$\frac{（b+a）（b-a）}{a}÷\frac{{a}^{2}-2ab+{b}^{2}}{a}$
=$\frac{（b+a）（b-a）}{a}•\frac{a}{（a-b）^{2}}$
=$\frac{b+a}{b-a}$，
当a=7，b=6时，原式=$\frac{6+7}{6-7}=-13$．
点评 本题考查分式的化简求值，解答本题的关键是明确分式化简求值的方法．
练习册系列答案
相关题目
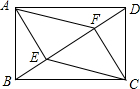如图，在矩形ABCD中，BD为对角线，点E，F是线段BD上的点，且BE=DF，连接AE，EC，CF，FA．
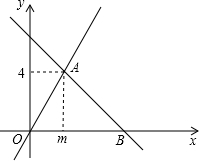如图，在平面直角坐标系xOy中，一次函数y=-x+n的图象与正比例函数y=2x的图象交于点A（m，4）．
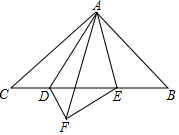已知：如图，△ABC中，∠CAB=90°，AC=AB，点D、E是BC上的两点，且∠DAE=45°，△ADC与△ADF关于直线AD对称．求证：（1）∠FAE=∠BAE；
琴琴在课外书上看到了如图所示的解方程的方法，请你按照如图所示的方法解下列方程组．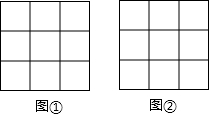
在边长为1个单位长度的小正方形组成的3×3的正方形网格图①、图②中，各画一个顶点在格点上的平行四边形，要求：每个平行四边形均为轴对称图形，每个平行四边形至少有一条边长为$\sqrt{5}$，所画的两个四边形不全等．