题目内容
20．
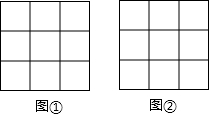在边长为1个单位长度的小正方形组成的3×3的正方形网格图①、图②中，各画一个顶点在格点上的平行四边形，要求：每个平行四边形均为轴对称图形，每个平行四边形至少有一条边长为$\sqrt{5}$，所画的两个四边形不全等．
分析 根据勾股定理以及结合菱形、正方形的性质得出符合题意的图形．
解答 解：如图所示：
．
点评 此题主要考查了轴对称变换以及勾股定理、特殊四边形的性质等知识，正确应用勾股定理是解题关键．
练习册系列答案
相关题目
在边长为1个单位长度的小正方形组成的3×3的正方形网格图①、图②中，各画一个顶点在格点上的平行四边形，要求：每个平行四边形均为轴对称图形，每个平行四边形至少有一条边长为$\sqrt{5}$，所画的两个四边形不全等．
如图，△ABC中，∠BAC=45°，AD⊥BC于D，BD=3，AD=8，求DC的长．