题目内容
18.【阅读材料,获取新知】善于思考的小军在解方程组
$\left\{\begin{array}{l}{2x+5y=3(1)}\\{4x+11y=5(2)}\end{array}\right.$时,采用了一种“整体代换法”的解法.
解:将方程(2)变形:4x+10y+y=5即2(2x+5y)+y=5(3)
把方程(1)代入(3)得:2×3+y=5
∴y=-1.
把y=-1,代入(1)得x=4
∴方程组的解为$\left\{\begin{array}{l}{x=4}\\{y=-1}\end{array}\right.$
【利用新知,解答问题】
请你利用小军的“整体代换法”解决一下问题:
(1)解方程组:
①$\left\{\begin{array}{l}{3x-2y=5}\\{9x-4y=19}\end{array}\right.$ ②$\left\{\begin{array}{l}{2x-3y-2=0}\\{\frac{2x-3y+5}{7}+2y=9}\end{array}\right.$
(2)已知x,y满足方程组$\left\{\begin{array}{l}{{3x}^{2}-2xy+1{2y}^{2}=47}\\{{2x}^{2}+xy+{8y}^{2}=36}\end{array}\right.$,则x2+4y2与xy的值分别为17、2.
分析 (1)①由②得出3(3x-2y)+2y=19③,把①代入③求出y,把y=2代入①求出x即可;
②整理方程组,由①得出2x-3y=2③,把③代入②得出1+2y=9,求出y,把y=4代入①求出x即可;
(2)原方程组化为$\left\{\begin{array}{l}{3({x}^{2}+4{y}^{2})-2xy=47①}\\{2({x}^{2}+4{y}^{2})+xy=36②}\end{array}\right.$,①+2×②求出x2+4y2,=17,把x2+4y2,=17代入①求出xy即可.
解答 解:(1)①$\left\{\begin{array}{l}{3x-2y=5①}\\{9x-4y=19②}\end{array}\right.$
由②得:3(3x-2y)+2y=19③,
把①代入③得:15+2y=19,
解得:y=2,把y=2代入①得:3x-4=5,
解得:x=3,
所以原方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$;
②$\left\{\begin{array}{l}{2x-3y-2=0①}\\{\frac{2x-3y+5}{7}+2y=9②}\end{array}\right.$
由①得:2x-3y=2③,
把③代入②得:1+2y=9,
解得:y=4,
把y=4代入①得:2x-12-2=0,
解得:x=7,
所以原方程组的解为$\left\{\begin{array}{l}{x=7}\\{y=4}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{{3x}^{2}-2xy+1{2y}^{2}=47}\\{{2x}^{2}+xy+{8y}^{2}=36}\end{array}\right.$,
原方程组化为:$\left\{\begin{array}{l}{3({x}^{2}+4{y}^{2})-2xy=47①}\\{2({x}^{2}+4{y}^{2})+xy=36②}\end{array}\right.$,
①+2×②得:7(x2+4y2)=119,
即x2+4y2,=17,
把x2+4y2,=17代入①得:51-2xy=47,
解得:xy=2,
故答案为:17,2.
点评 本题考查了解二元一次方程组,能把二元一次方程组转化成一元一次方程是解此题的关键,用了整体代入思想.

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 如图,直线a,b被直线c所截(即直线c与直线a,b都相交),且a∥b,若∠1=120°,则∠2的度数=60度.
如图,直线a,b被直线c所截(即直线c与直线a,b都相交),且a∥b,若∠1=120°,则∠2的度数=60度.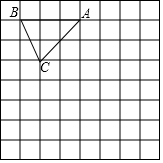 如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位,再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°,得到△A1B2C2.
如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位,再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°,得到△A1B2C2.