题目内容
6．
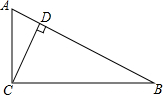如图，在Rt△ABC中，∠ACB=90°，AC=5cm，BC=12cm，其中斜边上的高为（ ）| A． | 6cm | B． | 8.5cm | C． | $\frac{60}{13}$cm | D． | $\frac{30}{13}$cm |
分析 根据勾股定理求出斜边AB的长，再根据直角三角形面积的两种不同求法列出关于CD的方程即可求解．
解答 解：∵在Rt△ABC中，AC=5cm，BC=12cm，
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{5}^{2}+1{2}^{2}}$=13cm；
∴S△ABC=$\frac{1}{2}$×5×12=30cm2；
∴$\frac{1}{2}$×13CD=30，解得CD=$\frac{60}{13}$cm．
故选C
点评 本题考查了勾股定理和三角形的面积公式，巧妙利用直角三角形两种面积求法是解题的关键．
练习册系列答案
教材全解字词句篇系列答案
相关题目
如图，点C、E和点B、D、F分别在∠GAH的两边上，且∠A=18°，AB=BC=CD=DE=EF，则∠GEF=90度．
15．△ABC中，AB=AC，∠A=∠C，则△ABC是（ ）
| A． | 等腰三角形 | B． | 等边三角形 | C． | 不等边三角形 | D． | 不能确定 |