题目内容
 如图所示,如果?ABCD的一内角∠BAD的平分线交BC于点E,且AE=BE,求?ABCD各内角的度数.
如图所示,如果?ABCD的一内角∠BAD的平分线交BC于点E,且AE=BE,求?ABCD各内角的度数.考点:平行四边形的性质
专题:
分析:由平行四边形ABCD中,∠BAD的平分线交BC于E,易得∠BAE=∠BEA,则AB=BE;又因为AE=BE,所以△ABE是等边三角形;即能求得∠BCD的度数.
解答: 解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠B+∠C=180°,∠AEB=∠DAE,
∵AE是∠BAD的平分线,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴AB=BE,
∵AE=BE,
∴△ABE是等边三角形,
∴∠B=60°,
∴∠BCD=120°.
∴?ABCD各内角的度数分别是:∠B=∠D=60°,∠BAD=∠C=120°.
 解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,
∴∠B+∠C=180°,∠AEB=∠DAE,
∵AE是∠BAD的平分线,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴AB=BE,
∵AE=BE,
∴△ABE是等边三角形,
∴∠B=60°,
∴∠BCD=120°.
∴?ABCD各内角的度数分别是:∠B=∠D=60°,∠BAD=∠C=120°.
点评:此题考查了平行四边形的性质:平行四边形的对边平行.还考查了等边三角形的判定与性质:等角对等边;等边三角形的三个角都等于60°,把四边形问题转化为三角形问题是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,以直角边为轴,把△ABC旋转1周,则所得几何体的全面积是( )
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,以直角边为轴,把△ABC旋转1周,则所得几何体的全面积是( )| A、20π |
| B、36π |
| C、15π或20π |
| D、24π或36π |
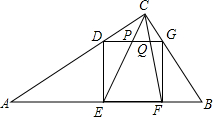 如图,△ABC中,∠C=90°,AC=4,BC=3,正方形DEFG的四个顶点分别在边AC、AB、CB上.
如图,△ABC中,∠C=90°,AC=4,BC=3,正方形DEFG的四个顶点分别在边AC、AB、CB上. 如图是一个正方体的表面展开图,如果正方体相对的面上标注的值相等,那么x+2y=
如图是一个正方体的表面展开图,如果正方体相对的面上标注的值相等,那么x+2y=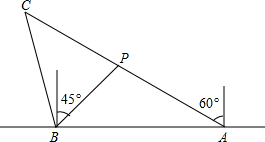 如图,海岸线l上有A,B两个观测站,A在B的正东方向,一艘船在点P处AP=6
如图,海岸线l上有A,B两个观测站,A在B的正东方向,一艘船在点P处AP=6 如图,在Rt△ABC中,∠C=90°,ED是线段AB的垂直平分线,∠A=
如图,在Rt△ABC中,∠C=90°,ED是线段AB的垂直平分线,∠A=