题目内容
 如图,在Rt△ABC中,∠C=90°,ED是线段AB的垂直平分线,∠A=
如图,在Rt△ABC中,∠C=90°,ED是线段AB的垂直平分线,∠A=| 1 |
| 3 |
考点:线段垂直平分线的性质
专题:
分析:根据垂直平分线的性质,得到BE=AE,进而得到∠EBD=∠EAB,设∠A=x°,根据直角三角形中两个锐角互余可得关于x的方程,解方程即可的问题答案.
解答:解:∵ED是AB边的垂直平分线,
∴BE=AE,
∴∠EBD=∠EAB,
设∠A=x°,
则∠CBE=∠EBD=∠A=x°,
∵∠C=90°,∠A=
∠ABC,
∴∠A+∠ABC=90°,即3x=90°,
解得x=30°,
∴∠A=30°.
∴BE=AE,
∴∠EBD=∠EAB,
设∠A=x°,
则∠CBE=∠EBD=∠A=x°,
∵∠C=90°,∠A=
| 1 |
| 3 |
∴∠A+∠ABC=90°,即3x=90°,
解得x=30°,
∴∠A=30°.
点评:本题主要考查了线段的垂直平分线的性质、直角三角形的两锐角互余、题目难度适中.

练习册系列答案
相关题目
△ABC中,∠C=90°,AC=1,AB=2,点O是AB的中点,直线l是线段AO的垂直平分线,那么下列命题中,错误的是( )
| A、直线l不经过点C |
| B、点C在直线l上 |
| C、直线l与AC边相交 |
| D、直线l与BC边相交 |
下列运算结果为正数的是( )
| A、2013-2014 |
| B、(-2014)3 |
| C、(-1)-(-2014) |
| D、-1+(-2014) |
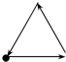
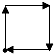
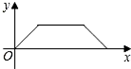 如图所示是李老师早晨出门散步时,离家的距离y与时间x之间的函数图象,若用黑点表示李老师家的位置,则李老师散步行走的路线可能是( )
如图所示是李老师早晨出门散步时,离家的距离y与时间x之间的函数图象,若用黑点表示李老师家的位置,则李老师散步行走的路线可能是( )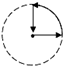

 如图所示,如果?ABCD的一内角∠BAD的平分线交BC于点E,且AE=BE,求?ABCD各内角的度数.
如图所示,如果?ABCD的一内角∠BAD的平分线交BC于点E,且AE=BE,求?ABCD各内角的度数. 在Rt△ABC中,∠C=90°,BC=
在Rt△ABC中,∠C=90°,BC=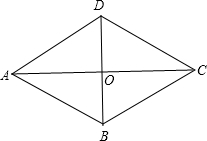 如图,?ABCD的对角线AC,BD相交于点O,且AB=10,AO=8,BO=6,求证?ABCD的菱形.
如图,?ABCD的对角线AC,BD相交于点O,且AB=10,AO=8,BO=6,求证?ABCD的菱形.