题目内容
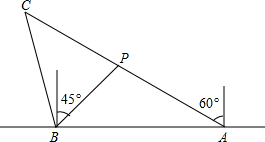 如图,海岸线l上有A,B两个观测站,A在B的正东方向,一艘船在点P处AP=6
如图,海岸线l上有A,B两个观测站,A在B的正东方向,一艘船在点P处AP=6| 2 |
(1)求点P到海岸线l的距离;
(2)船从点P处沿射线AP的方向航行一段时间后,到达点C处.此时,从B测得小船在北偏西15°的方向.求点C与点B之间的距离.(上述2小题的结果都保留根号)
考点:解直角三角形的应用-方向角问题
专题:
分析:(1)作PD⊥AB,垂足为D,根据PD=AP•sin30°即可得出结论;
(2)作BE⊥AC,根据△BDP为等腰直角三角形可知BD=PD,由锐角三角函数的定义可得出AD、BE的长,进而可得出CB的长.
(2)作BE⊥AC,根据△BDP为等腰直角三角形可知BD=PD,由锐角三角函数的定义可得出AD、BE的长,进而可得出CB的长.
解答: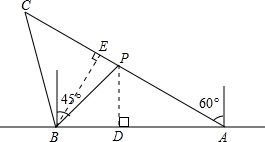 解:(1)作PD⊥AB,垂足为D.
解:(1)作PD⊥AB,垂足为D.
∵A测得船在北偏西60°的方向,
∴∠OAD=30°,
∴PD=AP•sin30°=6
×
=3
km.
答:点P到海岸线l的距离为3
km;
(2)作BE⊥AC,
∵△BDP为等腰直角三角形,
∴BD=PD=3
km,
∴AD=6
•cos30°=3
km.
∴BE=(3
+3
)sin30°=(
+
)km.
∴CB=(
+
)÷sin45°=(3+3
)km.
答:点C与点B之间的距离是(3+3
)km.
 解:(1)作PD⊥AB,垂足为D.
解:(1)作PD⊥AB,垂足为D.∵A测得船在北偏西60°的方向,
∴∠OAD=30°,
∴PD=AP•sin30°=6
| 2 |
| 1 |
| 2 |
| 2 |
答:点P到海岸线l的距离为3
| 2 |
(2)作BE⊥AC,
∵△BDP为等腰直角三角形,
∴BD=PD=3
| 2 |
∴AD=6
| 2 |
| 6 |
∴BE=(3
| 6 |
| 2 |
3
| ||
| 2 |
3
| ||
| 2 |
∴CB=(
3
| ||
| 2 |
3
| ||
| 2 |
| 3 |
答:点C与点B之间的距离是(3+3
| 3 |
点评:本题考查的是解直角三角形的应用-方向角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
在-(-2),|-3|,0,(-1)2,(-2)3这五个数中,正数的个数为( )
| A、1个 | B、2个 | C、3个 | D、4个 |
△ABC中,∠C=90°,AC=1,AB=2,点O是AB的中点,直线l是线段AO的垂直平分线,那么下列命题中,错误的是( )
| A、直线l不经过点C |
| B、点C在直线l上 |
| C、直线l与AC边相交 |
| D、直线l与BC边相交 |
 如图,△ABC的三个顶点坐标分别为A(-4,-2),B(-5,-4),C(0,-4),作一个平移,平面内任意一点P(x0,y0)的像是点P′(x0+7,y0+6),△ABC的像是△A′B′C′,求△A′B′C′的三个顶点A′,B′,C′的坐标.
如图,△ABC的三个顶点坐标分别为A(-4,-2),B(-5,-4),C(0,-4),作一个平移,平面内任意一点P(x0,y0)的像是点P′(x0+7,y0+6),△ABC的像是△A′B′C′,求△A′B′C′的三个顶点A′,B′,C′的坐标. 如图,在Rt△ABC中,∠C=90°,AD是△CAB的平分线,DE垂直平分AB,若CD=3,则BD=
如图,在Rt△ABC中,∠C=90°,AD是△CAB的平分线,DE垂直平分AB,若CD=3,则BD= 如图所示,如果?ABCD的一内角∠BAD的平分线交BC于点E,且AE=BE,求?ABCD各内角的度数.
如图所示,如果?ABCD的一内角∠BAD的平分线交BC于点E,且AE=BE,求?ABCD各内角的度数.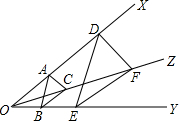 如图,点A,D在∠XOY的边OX上,点B,E在OY边上,射线OZ在∠XOY内,且点C,F在OZ上,AC∥DF,BC∥EF.
如图,点A,D在∠XOY的边OX上,点B,E在OY边上,射线OZ在∠XOY内,且点C,F在OZ上,AC∥DF,BC∥EF. 如图,在Rt△ABC中,∠C=90°,BC=4cm,AC=3cm,以边BC所在的直线为轴,将Rt△ABC
如图,在Rt△ABC中,∠C=90°,BC=4cm,AC=3cm,以边BC所在的直线为轴,将Rt△ABC