题目内容
10.已知点A(4,y1),B($\sqrt{2}$,y2),C(-2,y3)都在二次函数y=-(x-2)2+k的图象上,则y1,y2,y3的大小关系是y3<y1<y2.分析 先利用顶点式得到抛物线对称轴为直线x=2,再比较点A、B、C到直线x=2的距离,然后根据二次函数的性质判断函数值的大小.
解答 解:二次函数y=-(x-2)2+k的图象的对称轴为直线x=2,
因为点B($\sqrt{2}$,y2)到直线x=2的距离最小,点C(-2,y3)到直线x=2的距离最大,
而抛物线的开口向下,
所以y3<y1<y2.
故答案为y3<y1<y2.
点评 本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.熟练掌握二次函数的性质是解决本题的关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
20.对于二次函数y=2x2-8x+6的图象,下列说法正确的是( )
| A. | 开口向下 | B. | 与x轴的交点横坐标是x1=-1,x2=-3 | ||
| C. | 对称轴是直线x=-2 | D. | 由y=-2(x-2)2+2的图象轴对称得到 |
1.方程$\frac{0.5x+2}{0.03}-x=\frac{0.3(0.5x+2)}{0.2}$的解是( )
| A. | x=-$\frac{764}{179}$ | B. | x=$\frac{764}{179}$ | C. | x=-$\frac{765}{179}$ | D. | x=$\frac{765}{179}$ |
5.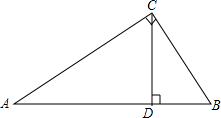 如图,在Rt△ABC中,∠C=90°,CD是斜边AB上的高,下列线段的比值不等于cosA的值的是( )
如图,在Rt△ABC中,∠C=90°,CD是斜边AB上的高,下列线段的比值不等于cosA的值的是( )
 如图,在Rt△ABC中,∠C=90°,CD是斜边AB上的高,下列线段的比值不等于cosA的值的是( )
如图,在Rt△ABC中,∠C=90°,CD是斜边AB上的高,下列线段的比值不等于cosA的值的是( )| A. | $\frac{AD}{AC}$ | B. | $\frac{AC}{AB}$ | C. | $\frac{BD}{BC}$ | D. | $\frac{CD}{BC}$ |
2. 如图,弦AC∥OB,∠B=25°,则∠O=( )
如图,弦AC∥OB,∠B=25°,则∠O=( )
 如图,弦AC∥OB,∠B=25°,则∠O=( )
如图,弦AC∥OB,∠B=25°,则∠O=( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
 (1)已知:如图,△ABC≌△A′B′C′,D是BC的中点,D′是B′C′的中点,求证:AD=A′D′;
(1)已知:如图,△ABC≌△A′B′C′,D是BC的中点,D′是B′C′的中点,求证:AD=A′D′;