题目内容
9. (1)已知:如图,△ABC≌△A′B′C′,D是BC的中点,D′是B′C′的中点,求证:AD=A′D′;
(1)已知:如图,△ABC≌△A′B′C′,D是BC的中点,D′是B′C′的中点,求证:AD=A′D′;(2)试用一个命题来表述(1)的结论,你能找一个类似的猜想吗?
分析 (1)根据△ABC≌△A′B′C′,可以得到AB和A′B′、∠B和∠B′、BC和B′C′的关系,从而可以得到AD和A′D′的关系;
(2)根据命题是由题设和结论组成,可以将(1)中的命题表述出来,从而可以解答本题.
解答 (1)证明:∵△ABC≌△A′B′C′,
∴AB=A′B′、∠B=∠B′、BC=B′C′,
∵D是BC的中点,D′是B′C′的中点,
∴BD=B′D′,
在△ABD和△A′B′D′中,
$\left\{\begin{array}{l}{AB=A′B′}\\{∠B=∠B′}\\{BD=B′D′}\end{array}\right.$,
∴△ABD≌△A′B′D′(SAS),
∴AD=A′D′;
(2)解:对(1)的描述是:如果两个三角形全等,那么对应边上的中线也相等;
猜想:如果两个三角形全等,那么对应边上的高也相等.
点评 本题考查全等三角形的判定和性质,解题的关键是由全等的性质可以得到我们所要证明结论需要的条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.钟表上的时间指示为1点20分,则它的时针与分针所成的角是( )
| A. | 110° | B. | 90° | C. | 80° | D. | 70° |
1.下列一元二次方程中,总有两个不相等实数根的是( )
| A. | 2x2+4x+2=0 | B. | x2+4x+5=0 | C. | x2+2014x-2015=0 | D. | 3x2+1=0 |
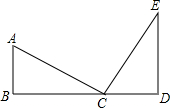 如图所示,点D为BC延长线上一点,点A,E是直线BC同侧的两点,∠B=90°,CD=AB,DE∥AB,AC⊥CE于C,求证:点C在线段AE的垂直平分线上.
如图所示,点D为BC延长线上一点,点A,E是直线BC同侧的两点,∠B=90°,CD=AB,DE∥AB,AC⊥CE于C,求证:点C在线段AE的垂直平分线上.