题目内容
12．如果反比例函数$y=\frac{m-2}{x}$的图象在二、四象限内，那么m的取值范围是m＜2．分析 根据反比例函数图象所在的象限结合反比例函数的性质，即可得出反比例函数系数k的正负，由此可得出关于m的一元一次不等式，解不等式即可得出结论．
解答 解：∵反比例函数$y=\frac{m-2}{x}$的图象在二、四象限内，
∴m-2＜0，
解得：m＜2．
故答案为：m＜2．
点评 本题考查了反比例函数的性质以及解一元一次不等式，解题的关键是找出m-2＜0．本题属于基础题，难度不大，解决该题型题目时，根据反比例函数图象所在的象限结合反比例函数的性质，找出反比例函数系数的正负是关键．
练习册系列答案
相关题目
2．菱形的周长为20cm，两个相邻的内角的度数之比为1：2，则较长的对角线的长度是（ ）
| A． | 20$\sqrt{3}$ | B． | 5$\sqrt{3}$cm | C． | $\frac{5}{2}$$\sqrt{3}$cm | D． | 5cm |
20．已知菱形的周长为40cm，两条对角线之比3：4，则菱形面积为（ ）
| A． | 96cm2 | B． | 48cm2 | C． | 24cm2 | D． | 12cm2 |
4．如果不等式$\left\{\begin{array}{l}{x＜5}\\{x＞m}\end{array}\right.$无解，那么m的取值范围是（ ）
| A． | m＜5 | B． | m≤5 | C． | m＞5 | D． | m≥5 |
1．
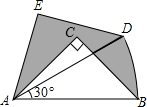如图，在Rt△ABC中，∠ACB=90°，AC=BC=1，将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE，点B经过的路径为BD，则图中阴影部分的面积是（ ）
如图，在Rt△ABC中，∠ACB=90°，AC=BC=1，将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE，点B经过的路径为BD，则图中阴影部分的面积是（ ）| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{2}$ | D． | $\frac{π}{3}$ |