题目内容
17.如果最简根式$\sqrt{3a-8}$与$\sqrt{17-2a}$是同类二次根式,那么使$\sqrt{4a-2x}$+$\frac{x}{x-3}$有意义的x的范围是x≤10且x≠3.分析 根据同类二次根式的定义求出x的值,再由二次根式及分式有意义的条件求出x的取值范围即可.
解答 解:∵最简根式$\sqrt{3a-8}$与$\sqrt{17-2a}$是同类二次根式,
∴3a-8=17-2a,解得a=5,
∴4a-2x=20-2x,
∵$\sqrt{4a-2x}$+$\frac{x}{x-3}$有意义,
∴$\left\{\begin{array}{l}20-2x≥0\\ x-3≠0\end{array}\right.$,解得x≤10且x≠3.
故答案为:x≤10且x≠3.
点评 本题考查的是二次根式有意义的条件,熟知二次根式具有非负性是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.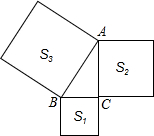 如图,在直角三角形ABC的三边上,向外做三个正方形,其中两个的面积为S3=169,S2=144,则另一个面积S1为( )
如图,在直角三角形ABC的三边上,向外做三个正方形,其中两个的面积为S3=169,S2=144,则另一个面积S1为( )
 如图,在直角三角形ABC的三边上,向外做三个正方形,其中两个的面积为S3=169,S2=144,则另一个面积S1为( )
如图,在直角三角形ABC的三边上,向外做三个正方形,其中两个的面积为S3=169,S2=144,则另一个面积S1为( )| A. | 50 | B. | 30 | C. | 25 | D. | 100 |
5.甲、乙两个仓库共存粮450吨,现从甲仓库运出存粮的60%,从乙仓库运出存粮的40%.结果乙仓库所余的粮食比甲仓库所余的粮食多30吨.若设甲仓库原来存粮x吨,乙仓库原来存粮y吨,则下列所列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{x+y=450}\\{(1-60%)x-(1-40%)y=30}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=450}\\{60%x-40%y=30}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=450}\\{(1-40%)y-(1-60%)x=30}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=450}\\{40%y-60%x=30}\end{array}\right.$ |
6.若点(3,4)是反比例函数y=$\frac{2m-2}{x}$图象上一点,则此函数图象必须经过点( )
| A. | (2,6) | B. | (2,-6) | C. | (4,-3) | D. | (3,-4) |
7.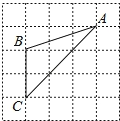 如图,已知△ABC的三个顶点均在格点上,则cosA的值为( )
如图,已知△ABC的三个顶点均在格点上,则cosA的值为( )
 如图,已知△ABC的三个顶点均在格点上,则cosA的值为( )
如图,已知△ABC的三个顶点均在格点上,则cosA的值为( )| A. | $\frac{1}{3}$$\sqrt{3}$ | B. | $\frac{1}{5}$$\sqrt{5}$ | C. | $\frac{2}{5}$$\sqrt{5}$ | D. | $\frac{2}{3}$$\sqrt{3}$ |