题目内容
10.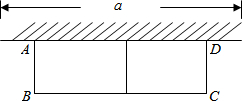 已知:如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度a为10米),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x米,面积为S米2.
已知:如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度a为10米),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x米,面积为S米2.(1)求S与x的函数关系式及自变量的取值范围;
(2)如果要围成面积为45米2的花圃,AB的长是多少米?
分析 (1)可先用篱笆的长表示出BC的长,然后根据矩形的面积=长×宽,得出S与x的函数关系式.根据墙的最大可用长度a为10米求出自变量的取值范围;
(2)根据(1)的函数关系式,将S=45代入其中,求出x的值即可.
解答 解:(1)由题可知,花圃的宽AB为x米,则BC为(24-3x)米.
这时面积S=x(24-3x)=-3x2+24x.
∵0<24-3x≤10,
∴$\frac{14}{3}$≤x<8,
即自变量的取值范围是$\frac{14}{3}$≤x<8;
(2)由条件-3x2+24x=45化为x2-8x+15=0,
解得x1=5,x2=3,
∵$\frac{14}{3}$≤x<8,
∴x=3不合题意,舍去,
即花圃的宽为5米.
点评 本题考查了一元二次方程,二次函数的综合应用,根据已知条件列出二次函数式是解题的关键.要注意题中自变量的取值范围不要丢掉.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.把抛物线y=-x2向左平移1个单位,然后向下平移3个单位,则平移后抛物线的解析式为( )
| A. | y=-(x-1)2-3 | B. | y=-(x-1)2+3 | C. | y=-(x+1)2-3 | D. | y=-(x+1)2+3 |
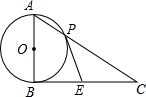 如图所示,AB是⊙O的直径,BC切⊙O于B,AC交⊙O于P,E是BC边上的中点,连结PE,求证:PE与⊙O相切.
如图所示,AB是⊙O的直径,BC切⊙O于B,AC交⊙O于P,E是BC边上的中点,连结PE,求证:PE与⊙O相切. 如图,已知D,E分别是△ABC的边AB、AC的延长线上的点,且DE∥BC,AB=5,BD=3,BC=6,求DE的长.
如图,已知D,E分别是△ABC的边AB、AC的延长线上的点,且DE∥BC,AB=5,BD=3,BC=6,求DE的长.