题目内容
10.已知m2+3m+2=0,n2+3n+2=0,$\frac{1}{n}$+$\frac{1}{m}$=-$\frac{3}{2}$.分析 由m2+3m+2=0,n2+3n+2=0,得到m,n是方程x2+3x+2=0的两个不等的根,根据根与系数的关系进行求解.
解答 解:∵m2+3m+2=0,n2+3n+2=0,
∴m,n是方程x2+3x+2=0的两个不相等的根,
∴m+n=-3,mn=2.
∴$\frac{1}{n}$+$\frac{1}{m}$
=$\frac{m+n}{mn}$
=-$\frac{3}{2}$.
故答案为:-$\frac{3}{2}$.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.

练习册系列答案
相关题目
18.已知$\frac{3}{{x}^{2}+x}$-x2=2+x,则代数式2x2+2x的值是( )
| A. | 2 | B. | -6 | C. | 2或-6 | D. | -2或6 |
5.已知,ab>0,化简二次根式a$\sqrt{-\frac{b}{{a}^{2}}}$的正确结果是( )
| A. | $\sqrt{b}$ | B. | $\sqrt{-b}$ | C. | -$\sqrt{b}$ | D. | -$\sqrt{-b}$ |
 如图,正方形ABCD中,在AD的延长线上取点E,F,使DE=AD,DF=BD,连接BF分别交CD,CE于H,G下列结论正确的有①③.(填序号)
如图,正方形ABCD中,在AD的延长线上取点E,F,使DE=AD,DF=BD,连接BF分别交CD,CE于H,G下列结论正确的有①③.(填序号)
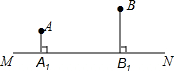 如图,直线MN表示一条铁路,A,B是两个城市,它们到铁路的垂直距离分别为AA1=20km,BB1=40km,已知A1B1=80km,现要在A1,B1之间设一个中转站P,使两个城市到中转站的距离之和最短,请你设计一种方案确定P点的位置,并求这个最短距离.
如图,直线MN表示一条铁路,A,B是两个城市,它们到铁路的垂直距离分别为AA1=20km,BB1=40km,已知A1B1=80km,现要在A1,B1之间设一个中转站P,使两个城市到中转站的距离之和最短,请你设计一种方案确定P点的位置,并求这个最短距离.