��Ŀ����
10������һ��Բ��һ�������θ������¶��壺��Բ�ϴ��ڵ��������������߾��붼��ȵĵ㣬������Բ�������εġ��Ⱦ�Բ����ͼ1����ƽ��ֱ������ϵxOy�У�������ABCD�Ķ���A������Ϊ��2��4��������C��D��x���ϣ��ҵ�C�ڵ�D����࣮
��1����r=2$\sqrt{2}$ʱ����P1��0��2����P2��-2��4����P3��4$\sqrt{2}$��2���п��Գ�Ϊ������ABCD�ġ��Ⱦ�Բ����Բ�ĵ���P2��P4��
��2����P������Ϊ��-3��6������P�İ뾶r=5ʱ����P��������ABCD�ġ��Ⱦ�Բ�������жϴ�ʱ��P��ֱ��AC��λ�ù�ϵ����˵�����ɣ�
��3����ͼ2����������ABCD����ƽ��ֱ������ϵxOy�У�������EFGH�Ķ���F������Ϊ��6��2��������E��H��y�����ҵ�H�ڵ�E���Ϸ���
�ٽ�������ABCD���ŵ�O��תһ�ܣ�����ת�Ĺ����У��߶�GF��û��һ�����ܳ�Ϊ���ġ��Ⱦ�Բ����Բ�ģ���r��ȡֵ��Χ��0��r��2$\sqrt{10}$-2��r��12��
������PͬʱΪ�������������εġ��Ⱦ�Բ��������BC����ֱ�����У����P��Բ��P�����꣮

���� ��1������AC��BD�����ڵ�M�����P��Բ�������ǣ�x��y�����г�Բ�ĵ�M�Ĺ�ϵʽ����P1��0��2����P2��-2��4����P3��4$\sqrt{2}$��2�����룬���Ƿ�������ж���
��2���ѵ�P��������루1����Բ�ķ��̿��������뾶�����ͼ2���ҵ�������ABCD������E�����ݵ�P��B��E��������֪�����㲻���ߣ���ֱ����Բ��λ�ù�ϵ���н��
��3��������DH����DT��HF����DΪԲ�ģ�DEΪ�뾶��Բ����DT�ڵ�E1����HD��E2����0��r��DT-DE1ʱ���߶�HF��û��һ�����ܳ�Ϊ���ġ��Ⱦ�Բ����Բ�ģ���r��HE2ʱ���߶�HF��û��һ�����ܳ�Ϊ���ġ��Ⱦ�Բ����Բ�ģ��ݴ���⣮
���������LIEΪ����ֱ�������Σ��õ�L��0��5���������ó���LOMΪ����ֱ�������Σ���P��p��-p+5���ݹ�ϵ�г���������Բ�ĵ����꣮
��� 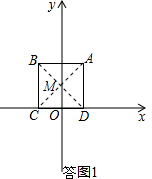 �⣺��1�����ͼ1������AC��BD�����ڵ�M��
�⣺��1�����ͼ1������AC��BD�����ڵ�M��
���ı���ABCD�������Σ�
��M��������ABCD�����߾��붼��ȣ�
���Pһ��ͨ����M��
��A��2��4��
��M��0��2��
���P��Բ�������ǣ�x��y����
��r=2$\sqrt{2}$ʱ��
��x2+��y-2��2=��2$\sqrt{2}$��2��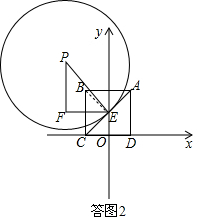
����x2+��y-2��2=8��
��P1��0��2����P2��-2��4����P3��4$\sqrt{2}$��2�����룬ֻ��P2��P4������
����Գ�Ϊ������ABCD�ġ��Ⱦ�Բ����Բ�ĵ���P2��P4��
�ʴ��ǣ�P2��P4��
��2��5���ҡ�P��ֱ��AC��λ�ù�ϵ���ཻ���������£�
��P�����꣨-3��6������x2+��y-2��2=��-3��2+��6-2��2=52�����Բ�İ뾶Ϊ5��
���ͼ2����������ABCD������ΪE����E��0��2����
��P��������-3��6������B��������-2��4����
���P��B��E����ͬһ��ֱ���ϣ�
�ߡ�CEB=90�㣬
���CEP��90�㣬
���P��AC�ľ����С��5��
���P��ֱ��AC��λ�ù�ϵ���ཻ��
��3�������ͼ3������DH����DT��HF����DΪԲ�ģ�DEΪ�뾶��Բ����DT�ڵ�E1����HD��E2��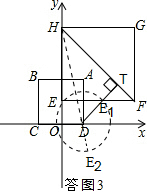 ��0��r��DT-DE1ʱ���߶�HF��û��һ�����ܳ�Ϊ���ġ��Ⱦ�Բ����Բ�ģ�
��0��r��DT-DE1ʱ���߶�HF��û��һ�����ܳ�Ϊ���ġ��Ⱦ�Բ����Բ�ģ�
��HF���ڵ�ֱ��Ϊ��y=-x+8��
DT���ڵ�ֱ��Ϊ��y=x-2��
��T��5��3����
��D��2��0����
��DT=$\sqrt{{3}^{2}+��5-2��^{2}}$=3$\sqrt{2}$��
��DE=DE1
��DT-DE1=DT-DE=3$\sqrt{2}$-2$\sqrt{2}$=$\sqrt{2}$��
�൱0��r��$\sqrt{2}$ʱ���߶�HF��û��һ�����ܳ�Ϊ���ġ��Ⱦ�Բ����Բ�ģ�
��r��HE2ʱ���߶�HF��û��һ�����ܳ�Ϊ���ġ��Ⱦ�Բ����Բ�ģ�
��HE2=HD+DE2��DE2=DE��
��HE2=HD+DE=$\sqrt{H{O}^{2}+O{D}^{2}}$+2$\sqrt{2}$=$\sqrt{{8}^{2}+{2}^{2}}$+2$\sqrt{2}$=2$\sqrt{17}$+2$\sqrt{2}$��
�൱r��2$\sqrt{17}$+2$\sqrt{2}$ʱ���߶�HF��û��һ�����ܳ�Ϊ���ġ��Ⱦ�Բ����Բ�ģ�
�ڡߡ�PͬʱΪ������ABCD��������EFGH�ġ��Ⱦ�Բ����
���Pͬʱ��������ABCD�ĶԳ�����E��������EFGH�ĶԳ�����I��
���P���߶�EI���д����ϣ�
��A��2��4����������ABCD�ı�CD��x���ϣ�F��6��2����������EFGH�ı�HE��y���ϣ�
��E��0��2����I��3��5��
���IEH=45�㣬
���߶�EI���д�����y�ύ�ڵ�L����x�ύ�ڵ�M��
���LIEΪ����ֱ�������Σ�LI��y�ᣬ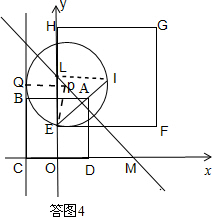
��L��0��5����
���LOMΪ����ֱ�������Σ�LO=OM
��M��5��0����
��P��ֱ��y=-x+5�ϣ�
����P��p��-p+5��
��P��PQ��ֱ��BC��Q������PE��
�ߡ�P��BC����ֱ�����У�
��PE=PQ��
��p2+��-p+5-2��2=��p+2��2��
��ã�p1=5+2$\sqrt{5}$��p2=5-2$\sqrt{5}$��
��P1��5+2$\sqrt{5}$��-2$\sqrt{5}$����P2��5-2$\sqrt{5}$��2$\sqrt{5}$����
���� ���⿼����Բ�ۺ��⣮һ��ҪŪ�������е���֪�����������еġ��Ⱦ�Բ���Ķ�������ȷ����Ĺؼ���

| A�� | 32��31 | B�� | 31��32 | C�� | 31��31 | D�� | 32��35 |
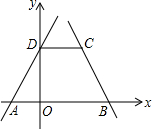 һ�κ���y=2x+2ͼ����x�ᡢy��ֱ���A��D���㣬һ�κ���y=-2x+8��x�ύ��B�㣬��D����DC��x�ᣬ��ֱ��y=-2x+8�ڵ�C��
һ�κ���y=2x+2ͼ����x�ᡢy��ֱ���A��D���㣬һ�κ���y=-2x+8��x�ύ��B�㣬��D����DC��x�ᣬ��ֱ��y=-2x+8�ڵ�C��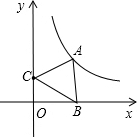 ��ͼ����A�Ƿ���������y=$\frac{5\sqrt{3}}{x}$��x��0��ͼ����һ�㣬��B��x����������һ�㣬��C������Ϊ��0��2��������ABC�ǵȱ�������ʱ����A������Ϊ��$\frac{3\sqrt{3}}{5}$��$\frac{25}{3}$����
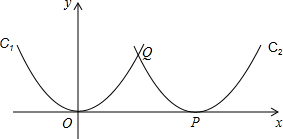
��ͼ����A�Ƿ���������y=$\frac{5\sqrt{3}}{x}$��x��0��ͼ����һ�㣬��B��x����������һ�㣬��C������Ϊ��0��2��������ABC�ǵȱ�������ʱ����A������Ϊ��$\frac{3\sqrt{3}}{5}$��$\frac{25}{3}$����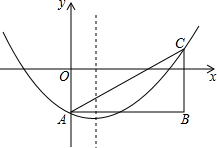 ��ͼ����ƽ��ֱ������ϵ�У�������y=ax2-2ax-2��a��0����y�ύ�ڵ�A����B������Ϊ��$\frac{1}{a}$��-2��������B��y���ƽ���ߣ����������ڵ�C������AB��AC��
��ͼ����ƽ��ֱ������ϵ�У�������y=ax2-2ax-2��a��0����y�ύ�ڵ�A����B������Ϊ��$\frac{1}{a}$��-2��������B��y���ƽ���ߣ����������ڵ�C������AB��AC��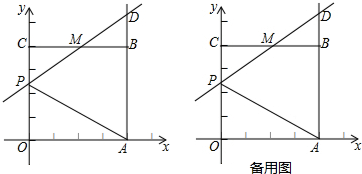
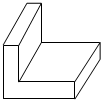 һ�����ڷ����L�ΰ�װ������ĭ��ͼ��ʾ���������ĸ���ͼ�ǣ�������
һ�����ڷ����L�ΰ�װ������ĭ��ͼ��ʾ���������ĸ���ͼ�ǣ�������