题目内容
13．已知mx+$\frac{1}{3}$y2n+1=-2是二元一次方程，则m≠0，n=0．分析 二元一次方程满足的条件：含有2个未知数，未知数的项的次数是1的整式方程．
解答 解：由mx+$\frac{1}{3}$y2n+1=-2是二元一次方程，得
$\left\{\begin{array}{l}{m≠0}\\{2n+1=0}\end{array}\right.$，
解得$\left\{\begin{array}{l}{m≠0}\\{n=0}\end{array}\right.$，
故答案为：≠0，0．
点评 主要考查二元一次方程的概念，要求熟悉二元一次方程的形式及其特点：含有2个未知数，未知数的项的次数是1的整式方程．
练习册系列答案
相关题目
3．
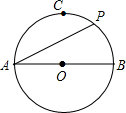如图，在⊙O中，AB是直径，点C是$\widehat{AB}$的中点，点P是$\widehat{BC}$上任意一点，则∠PAB的度数不可能为（ ）
如图，在⊙O中，AB是直径，点C是$\widehat{AB}$的中点，点P是$\widehat{BC}$上任意一点，则∠PAB的度数不可能为（ ）| A． | 0° | B． | 30° | C． | 45° | D． | 60° |
二次函数y=x2-8x+n的部分图象如图所示，若关于x的一元二次方程x2-8x+n=0的一个解为x1=1．则另一个解为x2=7．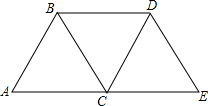
如图，把△ABC按AC方向平移，平移的距离是AC的长度，则平移后点B平移到点D，连接BD后，得到的四边形ACDB和CEDB都是平行四边形吗？
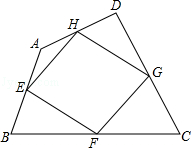如图，我们把依次连接任意四边形ABCD各边中点所得四边形EFGH叫中点四边形．