题目内容
3.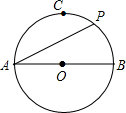 如图,在⊙O中,AB是直径,点C是$\widehat{AB}$的中点,点P是$\widehat{BC}$上任意一点,则∠PAB的度数不可能为( )
如图,在⊙O中,AB是直径,点C是$\widehat{AB}$的中点,点P是$\widehat{BC}$上任意一点,则∠PAB的度数不可能为( )| A. | 0° | B. | 30° | C. | 45° | D. | 60° |
分析 首先连接AC,BC,由在⊙O中,AB是直径,点C是$\widehat{AB}$的中点,可得△ABC是等腰直角三角形,又由点P是$\widehat{BC}$上任意一点,即可得0°≤∠PAB≤45°,继而求得答案.
解答  解:连接AC,BC,
解:连接AC,BC,
∵AB是直径,
∴∠ACB=90°,
∵点C是$\widehat{AB}$的中点,
∴AC=BC,
∴∠BAC=45°,
∵点P是$\widehat{BC}$上任意一点,
∴0°≤∠PAB≤45°.
故选D.
点评 此题考查了圆周角定理以及弧与弦的关系.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
18.平移小菱形◇可以得到美丽的“中国结”图案,下面四个图案是由◇平移后得到的类似“中国结”的图案,按图中规律,第20个图案中,小菱形的个数是( )


| A. | 780 | B. | 800 | C. | 820 | D. | 840 |
15.湿地观鸟、草莓采摘、海边烧烤是我市的特色旅游项目,今年“五一”期间我市共接待海内外游客24.1万人次,将24.1万用科学记数法可表示为( )
| A. | 2.41×106 | B. | 24.1×104 | C. | 2.41×104 | D. | 2.41×105 |
12.计算:a-2(1-3a)的结果为( )
| A. | 7a-2 | B. | -2-5a | C. | 4a-2 | D. | 2a-2 |
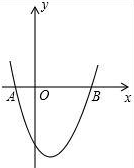 如图,抛物线y=x2-x-2交x轴于A(-1,0),B两点,交y轴于C(0,-2),过A,C画直线.点M在抛物线上,以M为圆心的圆与直线AC相切,切点为H,若⊙M的半径为$\frac{4\sqrt{5}}{5}$,求点M的坐标.
如图,抛物线y=x2-x-2交x轴于A(-1,0),B两点,交y轴于C(0,-2),过A,C画直线.点M在抛物线上,以M为圆心的圆与直线AC相切,切点为H,若⊙M的半径为$\frac{4\sqrt{5}}{5}$,求点M的坐标. 如图,正方形ABCD的正方形CEFG的面积分别是7和5.
如图,正方形ABCD的正方形CEFG的面积分别是7和5.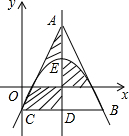 如图,点E是抛物线y=a(x-2)2+k的顶点,抛物线与y轴交于点C,过点C作CD∥x轴,与抛物线交于点B,与对称轴交于点D.点A是对称轴上一点,连结AC、AB.若△ABC是等边三角形,则图中阴影部分图形的面积之和是2$\sqrt{3}$.
如图,点E是抛物线y=a(x-2)2+k的顶点,抛物线与y轴交于点C,过点C作CD∥x轴,与抛物线交于点B,与对称轴交于点D.点A是对称轴上一点,连结AC、AB.若△ABC是等边三角形,则图中阴影部分图形的面积之和是2$\sqrt{3}$.