题目内容
 如图,在?ABCD中,EF过对角线交点O,分别交AD,BC于点E,F,点G,H分别是OA与OC的中点,试判断四边形EGFH的形状,并证明你的结论.
如图,在?ABCD中,EF过对角线交点O,分别交AD,BC于点E,F,点G,H分别是OA与OC的中点,试判断四边形EGFH的形状,并证明你的结论.考点:平行四边形的判定与性质
专题:
分析:可先证明△EOD≌△FOB,可证明OE=OF,结合条件和平行四边形的性质可证得OG=OH,可证明四边形EGFH为平行四边形.
解答: 解:四边形EGFH为平行四边形,证明如下:
解:四边形EGFH为平行四边形,证明如下:
∵四边形ABCD为平行四边形,
∴AD∥BC,OB=OD,∠EDO=∠FBO,
∴∠DEO=∠BFO,
在△EOD和△BOF中,
,
∴△EOD≌△FOB(AAS),
∴OE=OF,
∵点G,H分别是OA与OC的中点,
∴GO=
OA,HO=
OC,
又∵由平行四边形的性质可得OA=OC,
∴OG=OH,
∴四边形EGFH为平行四边形.
 解:四边形EGFH为平行四边形,证明如下:
解:四边形EGFH为平行四边形,证明如下:∵四边形ABCD为平行四边形,
∴AD∥BC,OB=OD,∠EDO=∠FBO,
∴∠DEO=∠BFO,
在△EOD和△BOF中,
|
∴△EOD≌△FOB(AAS),
∴OE=OF,
∵点G,H分别是OA与OC的中点,
∴GO=
| 1 |
| 2 |
| 1 |
| 2 |
又∵由平行四边形的性质可得OA=OC,
∴OG=OH,
∴四边形EGFH为平行四边形.
点评:本题主要考查平行四边形的判定和性质,掌握平行四边形的判定和性质是解题的关键,即①两组对边分别平行的四边形?平行四边形,②两组对边分别相等的四边形?平行四边形,③一组对边平行且相等的四边形?平行四边形,④两组对角分别相等的四边形?平行四边形,⑤对角线互相平分的四边形?平行四边形.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 如图,已知⊙O的半径为5,弦AB的长为8,半径OD过AB的中点C,则OC的长为( )
如图,已知⊙O的半径为5,弦AB的长为8,半径OD过AB的中点C,则OC的长为( )| A、2 | B、3 | C、4 | D、5 |
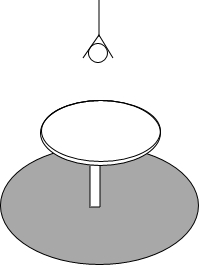 如图所示,直径为40cm的一张小圆桌桌面距离地面50cm,距离其正上方的一盏电灯的距离也是50cm
如图所示,直径为40cm的一张小圆桌桌面距离地面50cm,距离其正上方的一盏电灯的距离也是50cm 如图,双曲线y=
如图,双曲线y= 如图,AD⊥BC,垂足为D,点E在AC上,∠EBC=40°,∠A=30°,求∠BEC的度数.
如图,AD⊥BC,垂足为D,点E在AC上,∠EBC=40°,∠A=30°,求∠BEC的度数. 已知:如图,9×9的网格中(每个小正方形的边长为1)有一个格点△ABC.
已知:如图,9×9的网格中(每个小正方形的边长为1)有一个格点△ABC. 如图,△ABC是一块锐角三角形材料,边BC=40cm,高AD=30cm,要把它加工成矩形零件,矩形EFGH的一边FG在BC上,其余两个顶点分别在AB、AC上,AD与EH的交点为点M,设FG=x cm,当x为何值时,这个矩形零件的面积最大?最大面积是多少?
如图,△ABC是一块锐角三角形材料,边BC=40cm,高AD=30cm,要把它加工成矩形零件,矩形EFGH的一边FG在BC上,其余两个顶点分别在AB、AC上,AD与EH的交点为点M,设FG=x cm,当x为何值时,这个矩形零件的面积最大?最大面积是多少?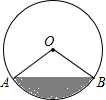 如图,有一个马戏帐篷,它的底部是圆形,其半径为20m,从a到b有一笔直的栅栏,其长为30m,观众在阴影区域里看马戏,如果每平方米可以坐三名观众,并且阴影区域坐满了人,那么大约有多少名观众在看马戏?
如图,有一个马戏帐篷,它的底部是圆形,其半径为20m,从a到b有一笔直的栅栏,其长为30m,观众在阴影区域里看马戏,如果每平方米可以坐三名观众,并且阴影区域坐满了人,那么大约有多少名观众在看马戏?