题目内容
2.如果实数x、y满足方程组$\left\{\begin{array}{l}{x-y=\frac{3}{2}}\\{2x+2y=5}\end{array}\right.$,那么x2-y2的值为$\frac{15}{4}$.分析 将第二个方程除以2得x+y=$\frac{5}{2}$,再将x+y、x-y的值代入x2-y2=(x+y)(x-y)可得答案.
解答 解:$\left\{\begin{array}{l}{x-y=\frac{3}{2}}&{①}\\{2x+2y=5}&{②}\end{array}\right.$
由②得x+y=$\frac{5}{2}$,
则x2-y2=(x+y)(x-y)=$\frac{3}{2}$×$\frac{5}{2}$=$\frac{15}{4}$,
故答案为:$\frac{15}{4}$.
点评 本题主要考查解二元一次方程组,观察到方程组中两个方程的特点及熟练掌握平方差公式是解题的关键.

练习册系列答案
相关题目
9.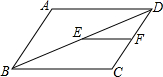 如图,在平行四边形ABCD中,AD=16,点E、F分别是BD、CD的中点,则EF的长为( )
如图,在平行四边形ABCD中,AD=16,点E、F分别是BD、CD的中点,则EF的长为( )
 如图,在平行四边形ABCD中,AD=16,点E、F分别是BD、CD的中点,则EF的长为( )
如图,在平行四边形ABCD中,AD=16,点E、F分别是BD、CD的中点,则EF的长为( )| A. | 6 | B. | $\frac{16}{3}$ | C. | 8 | D. | 9 |
7.下列事件:①调查长江现有鱼的数量;②学校为七年级学生订制校服要了解每位新生的上衣和裤子的尺寸; ③要检测一批灯泡的使用寿命;④校正某本书上的印刷错误. 最适合做全面调查的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.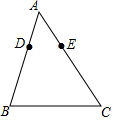 如图,在△ABC中,已知D、E分别是AB、AC边上的点,且AD=3,AB=8,AC=10,若△ADE与△ABC相似,则AE的长为( )
如图,在△ABC中,已知D、E分别是AB、AC边上的点,且AD=3,AB=8,AC=10,若△ADE与△ABC相似,则AE的长为( )
 如图,在△ABC中,已知D、E分别是AB、AC边上的点,且AD=3,AB=8,AC=10,若△ADE与△ABC相似,则AE的长为( )
如图,在△ABC中,已知D、E分别是AB、AC边上的点,且AD=3,AB=8,AC=10,若△ADE与△ABC相似,则AE的长为( )| A. | $\frac{15}{4}$ | B. | $\frac{4}{15}$或$\frac{12}{5}$ | C. | $\frac{15}{4}$或$\frac{12}{5}$ | D. | $\frac{5}{12}$ |
11.不透明的袋子中装有10个黑球、1个白球,它们除颜色外无其它差别,随机从袋子中摸出一个球,则( )
| A. | 这个球一定是黑球 | B. | 事先能确定摸到什么颜色的球 | ||
| C. | 这个球可能是白球 | D. | 摸到黑球、白球的可能性大小一样 |
12.点A(x1,y1)和B(x2,y2)在y=$\frac{4}{x}$的图象上,若x1>x2,则( )
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 无法比较 |
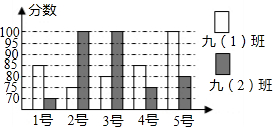 某中学开展“唱红歌”歌唱比赛,九年级(1)班、九年级(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示:
某中学开展“唱红歌”歌唱比赛,九年级(1)班、九年级(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示: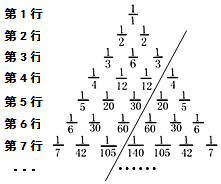 如图是“分数三角形”数表,记第i行从左往右数第j个数为ai,j(其中i、j均为正整数且j≤i),如a5,2=$\frac{1}{20}$,a7,6=$\frac{1}{42}$;请认真观察此数表的规律并完成下列作答.
如图是“分数三角形”数表,记第i行从左往右数第j个数为ai,j(其中i、j均为正整数且j≤i),如a5,2=$\frac{1}{20}$,a7,6=$\frac{1}{42}$;请认真观察此数表的规律并完成下列作答.