题目内容
17.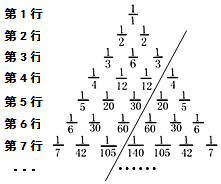 如图是“分数三角形”数表,记第i行从左往右数第j个数为ai,j(其中i、j均为正整数且j≤i),如a5,2=$\frac{1}{20}$,a7,6=$\frac{1}{42}$;请认真观察此数表的规律并完成下列作答.
如图是“分数三角形”数表,记第i行从左往右数第j个数为ai,j(其中i、j均为正整数且j≤i),如a5,2=$\frac{1}{20}$,a7,6=$\frac{1}{42}$;请认真观察此数表的规律并完成下列作答.(1)第10行的第一个数为$\frac{1}{10}$,第10行的第二个数为$\frac{1}{90}$;
(2)我发现了此数表有以下规律:
①第i行的第一个数与最后一个数均为$\frac{1}{i}$(用字母i来表示);
②请仔细观察每行相邻两个数与它们头顶上的那个数的关系,并完成下面填空:ai,2+ai,3=a(i-1),2(其中i为正整数且i≥3);
(3)请利用第(2)问②的规律计算:$\frac{1}{3}+\frac{1}{12}+\frac{1}{30}+\frac{1}{60}+\frac{1}{105}$.(请给出运算过程)
分析 (1)根据数表的规律,即可得出第10行的第一个数以及第二个数;
(2)①根据数表的规律,即可得出第i行的第一个数与最后一个数;
②根据每行相邻两个数的和等于它们头顶上的那个数,即可得到ai,2+ai,3=a(i-1),2;
(3)利用第(2)问②的规律进行计算,即可得到计算结果.
解答 解:(1)根据每一行的第一个数的分母与行数相同,可得第10行的第一个数为$\frac{1}{10}$;
根据每一行的第二个数的分母是第一个数的分母与前一行的第一个数的分母的乘积,可得第10行的第二个数为$\frac{1}{90}$;
故答案为:$\frac{1}{10}$,$\frac{1}{90}$;
(2)①由数表可知,第i行的第一个数与最后一个数均为$\frac{1}{i}$;
②根据数表可得,每行相邻两个数的和等于它们头顶上的那个数,故ai,2+ai,3=a(i-1),2;
故答案为:$\frac{1}{i}$,a(i-1),2;
(3)$\frac{1}{3}+\frac{1}{12}+\frac{1}{30}+\frac{1}{60}+\frac{1}{105}$
=$(\frac{1}{2}-\frac{1}{6})+(\frac{1}{6}-\frac{1}{12})+(\frac{1}{12}-\frac{1}{20})+(\frac{1}{20}-\frac{1}{30})+(\frac{1}{30}-\frac{1}{42})$
=$\frac{1}{2}-\frac{1}{42}$
=$\frac{10}{21}$.
点评 本题主要考查了数字变化类问题,发现规律,运用规律是解答此题的关键.认真观察、仔细思考,善用联想是解决这类问题的方法.

练习册系列答案
相关题目
4. 如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )
如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )
 如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )
如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )| A. | 两点之间,线段最短 | B. | 经过一点有无数条直线 | ||
| C. | 经过两点,有且只有一条直线 | D. | 部分小于总体 |
8.已知C是AB的中点,D是BC 的中点,下面等式不正确的是( )
| A. | CD=AC-DB | B. | CD=AD-BC | C. | CD=$\frac{1}{2}$AB-BD | D. | CD=$\frac{1}{3}$AB |
12.下列计算正确的是( )
| A. | x4+x4=x8 | B. | (x2y)3=x6y | C. | -x3•(-x)5=x8 | D. | m5÷m2×m=m2 |
9.下列说法正确的是( )
| A. | 1的平方根是1 | B. | 0没有平方根 | ||
| C. | 0.01是0.1的一个平方根 | D. | 1是1的一个平方根 |
7.在一个不透明的袋子中,有3个白球和2个红球,它们只有颜色上的区别,从袋子中随机地摸出1个球,摸到白球的概率为( )
| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |

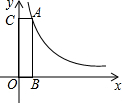 如图,过反比例函数y=$\frac{4}{x}$(x>0)上一点A作AB⊥x轴于点B,AC⊥y轴于点C,则四边形OBAC的面积是( )
如图,过反比例函数y=$\frac{4}{x}$(x>0)上一点A作AB⊥x轴于点B,AC⊥y轴于点C,则四边形OBAC的面积是( )