题目内容
13.已知代数式$\frac{1}{x-1}$+$\frac{{x}^{2}-3x}{{x}^{2}-1}$,回答下列问题.(1)化简这个代数式;
(2)“当x=1时,该代数式的值为0”,这个说法正确吗?请说明理由.
分析 (1)根据分式的性质,可化简成同分母分式,根据分式的加减,可得答案;
(2)根据代数式求值,可得答案.
解答 解:(1)原式=$\frac{x+1+{x}^{2}-3x}{{x}^{2}-1}$=$\frac{x-1}{x+1}$;
(2)当x=1时,该代数式的值为0”,这个说法不正确,理由如下
当x=1时,$\frac{1}{x-1}$+$\frac{{x}^{2}-3x}{{x}^{2}-1}$无意义.
点评 本题考查了分式的加减,利用分式的性质化简成同分母分式是解题关键.

练习册系列答案
相关题目
1.比$\frac{4}{7}$大且比$\frac{6}{7}$小的分数有( )
| A. | 一个 | B. | 两个 | C. | 无数个 | D. | 不存在 |
8.已知C是AB的中点,D是BC 的中点,下面等式不正确的是( )
| A. | CD=AC-DB | B. | CD=AD-BC | C. | CD=$\frac{1}{2}$AB-BD | D. | CD=$\frac{1}{3}$AB |
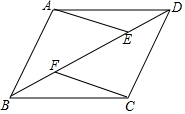 如图,?ABCD中,点E、F在BD上,且BF=DE.请连接AF、CE,并证明四边形AFCE是平行四边形.
如图,?ABCD中,点E、F在BD上,且BF=DE.请连接AF、CE,并证明四边形AFCE是平行四边形.