题目内容
11.计算:(1)(2$\sqrt{2}$-3)2013(2$\sqrt{2}$+3)2013=-1.
(2)($\sqrt{2}-1$)2=3-2$\sqrt{2}$.
(3)(3$\sqrt{2}$-2$\sqrt{3}$)(3+$\sqrt{6}$)=3$\sqrt{2}$.
分析 (1)利用积的乘方法则把原式变形,根据平方差公式计算即可;
(2)根据完全平方公式计算;
(3)根据多项式乘多项式的法则计算.
解答 解:(1)(2$\sqrt{2}$-3)2013(2$\sqrt{2}$+3)2013=[(2$\sqrt{2}$-3)(2$\sqrt{2}$+3)]2013=(8-9)2013=-1;
(2)($\sqrt{2}-1$)2=2-2$\sqrt{2}$+1=3-2$\sqrt{2}$;
(3)(3$\sqrt{2}$-2$\sqrt{3}$)(3+$\sqrt{6}$)=9$\sqrt{2}$+6$\sqrt{3}$-6$\sqrt{3}$-6$\sqrt{2}$=3$\sqrt{2}$.
故答案为:(1)-1;(2)3-2$\sqrt{2}$;(3)3$\sqrt{2}$.
点评 本题考查的是二次根式的混合运算,掌握积的乘方法则、平方差公式和完全平方公式是解题的关键,注意二次根式的加减乘除运算法则的灵活运用.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
3.计算$\sqrt{12}$÷$\sqrt{\frac{27}{2}}$×$\sqrt{\frac{1}{36}}$的值为( )
| A. | $\sqrt{3}$ | B. | $\frac{3}{2}$$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{9}$ | D. | $\frac{3}{2}$ |
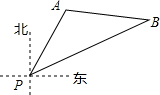 如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔20海里的A处,它沿正东方向航行一段时间后,到达位于灯塔P的北偏东60°方向上的B处,则此时轮船与灯塔的距离BP为20$\sqrt{3}$海里.
如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔20海里的A处,它沿正东方向航行一段时间后,到达位于灯塔P的北偏东60°方向上的B处,则此时轮船与灯塔的距离BP为20$\sqrt{3}$海里.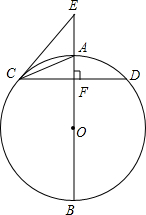 如图,已知AB为⊙O的直径,弦CD⊥AB,垂足为F,E为BA延长线上的一点,连接CE、CA,∠ECA=∠ACD.
如图,已知AB为⊙O的直径,弦CD⊥AB,垂足为F,E为BA延长线上的一点,连接CE、CA,∠ECA=∠ACD.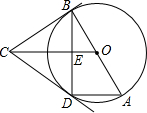 如图,已知AB是⊙O的直径,BC是⊙O的切线,B是切点,⊙O的弦AD∥OC.
如图,已知AB是⊙O的直径,BC是⊙O的切线,B是切点,⊙O的弦AD∥OC.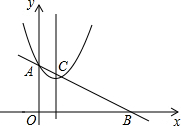 如图,在平面直角坐标系中,抛物线y=x2-2x+2交y轴于点A,直线AB交x轴正半轴于点B,交抛物线的对称轴于点C,若OB=2OA,则点C的坐标为(1,$\frac{3}{2}$).
如图,在平面直角坐标系中,抛物线y=x2-2x+2交y轴于点A,直线AB交x轴正半轴于点B,交抛物线的对称轴于点C,若OB=2OA,则点C的坐标为(1,$\frac{3}{2}$).