题目内容
20.如果$\sqrt{7a+2}$与$\sqrt{3a+14}$是同类二次根式,则a=3.分析 根据最简二次根式和同类二次根式的定义,列方程求解.
解答 解:因为$\sqrt{7a+2}$与$\sqrt{3a+14}$是同类二次根式,
可得:7a+2=3a+14,
解得:a=3,
故答案为:3.
点评 此题主要考查了同类二次根式的定义,即:化成最简二次根式后,被开方数相同的二次根式叫做同类二次根式.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
11.(6x-2y)2•(-xy)-2=( )
| A. | 36x-6 | B. | 36x-3 | C. | -12x-2y4 | D. | -36x-3y |
8.在下列各组二次根式中,不是可以合并的二次根式的一组是( )
| A. | $\sqrt{3ab^2}$和$\sqrt{3ab^2c}$ | B. | $\sqrt{12ab^3}$和$\sqrt{3ab}$ | C. | $\sqrt{ab}$和$\sqrt{{a}^{3}{b}^{5}}$ | D. | $\sqrt{\frac{b}{a}}$和$\sqrt{\frac{a}{b}}$ |
5.利用二次函数y=x2-2x-2的图象求一元二次方程y=x2-2x-2的近似解时,画图如图1示并进一步估算其中一根列表如下,根据这些信息,可得方程的正的近似根是( )
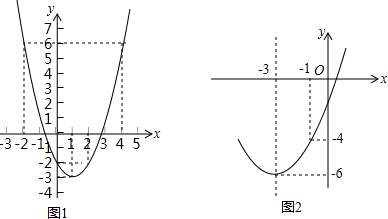
| x | -0.9 | -0.8 | -0.7 | -0.6 |
| y=x2-2x-2 | -0.61 | 0.24 | -0.11 | -0.44 |

| A. | 0.7 | B. | 2.6 | C. | 2.7 | D. | 2.8 |
7.如图,是由几个相同的小正方体搭成的几何体的三种视图,则搭成这个几何体的小正方体的个数是( )
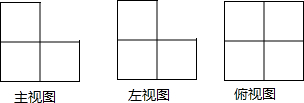

| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
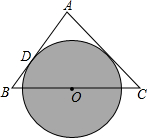 如图,在△ABC中,AB=AC,O是BC的中点,以O为圆心的⊙O切AB于D,求证:AC是⊙O的切线.(提示:证明切线的基本思路:不知共点,作垂直,证半径)
如图,在△ABC中,AB=AC,O是BC的中点,以O为圆心的⊙O切AB于D,求证:AC是⊙O的切线.(提示:证明切线的基本思路:不知共点,作垂直,证半径) 完成下面证明
完成下面证明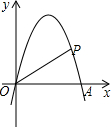 如图,在平面直角坐标系中,抛物线y=-x2+4x与x轴交于点O、A,点P在抛物线上,连结OP、AP,设点P的横坐标为m,△AOP的面积为S,若0<m<3,则S的取值范围是0<S≤8.
如图,在平面直角坐标系中,抛物线y=-x2+4x与x轴交于点O、A,点P在抛物线上,连结OP、AP,设点P的横坐标为m,△AOP的面积为S,若0<m<3,则S的取值范围是0<S≤8.