题目内容
2.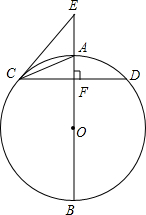 如图,已知AB为⊙O的直径,弦CD⊥AB,垂足为F,E为BA延长线上的一点,连接CE、CA,∠ECA=∠ACD.
如图,已知AB为⊙O的直径,弦CD⊥AB,垂足为F,E为BA延长线上的一点,连接CE、CA,∠ECA=∠ACD.(1)求证:CE为⊙O的切线;
(2)若EA=2,tanE=$\frac{3}{4}$,求⊙O的半径.
分析 (1)由AB为⊙O的直径,弦CD⊥AB,得到$\widehat{AC}$=$\widehat{AD}$,∠ACD=∠ABC,结合∠OCB+∠OCA=90°即可;
(2)在Rt△ECO中,tan∠E=$\frac{3}{4}$,设OC=R,得到CE=$\frac{4}{3}$R,OE=R+2即可.
解答 (1)证明:连接BC,OC,
∵AB为⊙O的直径,弦CD⊥AB,
∴$\widehat{AC}$=$\widehat{AD}$,
∴∠ACD=∠ABC,
∵OB=OC,
∴∠ABC=∠OCB,
∴∠ACD=∠OCB,
∵∠ECA=∠ACD.
∴∠EAC=∠OCB,
∵∠OCB+∠OCA=90°,
∴∠ECA+∠OCA=90°,
∴∠OCE=90°,
∵点C在⊙O上,
∴CE是⊙O的切线.
(2)在Rt△ECO中,tan∠E=$\frac{3}{4}$,设OC=R,
∴CE=$\frac{4}{3}$R,OE=R+2,
∴($\frac{4}{3}$R)2+R2=(R+2)2,
∴R=3或R=-$\frac{3}{4}$(舍).
点评 此题是切线的判定,涉及到圆中的性质,弦切角,勾股定理,判断∠OCE=90°是解本题的关键,

练习册系列答案
相关题目
7.如图,是由几个相同的小正方体搭成的几何体的三种视图,则搭成这个几何体的小正方体的个数是( )
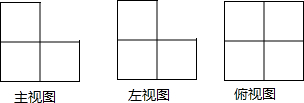

| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
 完成下面证明
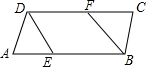
完成下面证明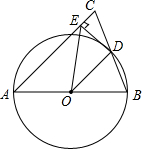 如图,△ABC中,AB=AC,以AB为直径作⊙0,交BC于D,DE⊥AC于E,连接0E.
如图,△ABC中,AB=AC,以AB为直径作⊙0,交BC于D,DE⊥AC于E,连接0E.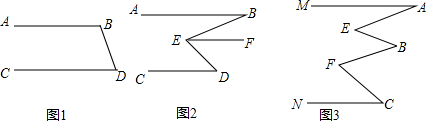
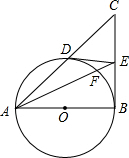 如图,在△ABC中,∠B=90°,以AB为直径的⊙O交AC于D,过点D作⊙O的切线交BC于E,AE交⊙O于点F.
如图,在△ABC中,∠B=90°,以AB为直径的⊙O交AC于D,过点D作⊙O的切线交BC于E,AE交⊙O于点F.