题目内容
19.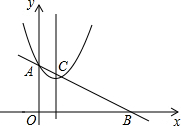 如图,在平面直角坐标系中,抛物线y=x2-2x+2交y轴于点A,直线AB交x轴正半轴于点B,交抛物线的对称轴于点C,若OB=2OA,则点C的坐标为(1,$\frac{3}{2}$).
如图,在平面直角坐标系中,抛物线y=x2-2x+2交y轴于点A,直线AB交x轴正半轴于点B,交抛物线的对称轴于点C,若OB=2OA,则点C的坐标为(1,$\frac{3}{2}$).
分析 由抛物线的解析式求得A(0,2)和对称轴x=1,进而求得B的坐标,然后根据待定系数法求得直线AB的解析式,把x=1代入即可求得.
解答 解:由抛物线y=x2-2x+2=(x-1)2+1可知A(0,2),对称轴为x=1,
∴OA=2,
∵OB=2OA,
∴B(4,0),
设直线AB的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{b=2}\\{4k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=2}\end{array}\right.$,
∴直线AB为y=-$\frac{1}{2}$x+2,
当x=1时,y=$\frac{3}{2}$,
∴C(1,$\frac{3}{2}$).
点评 本题考查了二次函数的性质以及待定系数法求一次函数的解析式,利用抛物线的解析式求A的坐标和对称轴是解题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
6.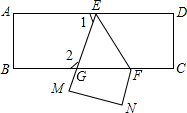 把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在MN的位置上,若∠EFG=55°,则∠2=( )
把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在MN的位置上,若∠EFG=55°,则∠2=( )
 把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在MN的位置上,若∠EFG=55°,则∠2=( )
把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在MN的位置上,若∠EFG=55°,则∠2=( )| A. | 105 | B. | 110 | C. | 95 | D. | 120 |
7.下列四个命题中,真命题是( )
| A. | 对角线互相垂直平分的四边形是正方形 | |
| B. | 对角线相等且互相平分的四边形是矩形 | |
| C. | 对角线垂直相等的四边形是菱形 | |
| D. | 四边都相等的四边形是正方形 |
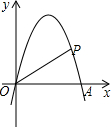 如图,在平面直角坐标系中,抛物线y=-x2+4x与x轴交于点O、A,点P在抛物线上,连结OP、AP,设点P的横坐标为m,△AOP的面积为S,若0<m<3,则S的取值范围是0<S≤8.
如图,在平面直角坐标系中,抛物线y=-x2+4x与x轴交于点O、A,点P在抛物线上,连结OP、AP,设点P的横坐标为m,△AOP的面积为S,若0<m<3,则S的取值范围是0<S≤8.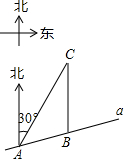 如图,某市郊外景区内一条笔直的公路a经过A、B两个景点,景区管委会又开发了风景优美的景点C,经测量,B位于A的北偏东75°方向,C位于B的正北方向,C位于A的北偏东30°方向,AB=8km.
如图,某市郊外景区内一条笔直的公路a经过A、B两个景点,景区管委会又开发了风景优美的景点C,经测量,B位于A的北偏东75°方向,C位于B的正北方向,C位于A的北偏东30°方向,AB=8km.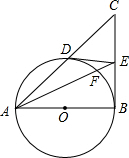 如图,在△ABC中,∠B=90°,以AB为直径的⊙O交AC于D,过点D作⊙O的切线交BC于E,AE交⊙O于点F.
如图,在△ABC中,∠B=90°,以AB为直径的⊙O交AC于D,过点D作⊙O的切线交BC于E,AE交⊙O于点F.