题目内容
17．
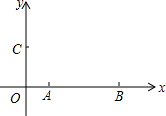如图，在平面直角坐标系中，点A的坐标为（1，0），点B的坐标为（4，0），点C在y的正半轴上，且OB=2OC，在直角坐标平面内确定点D，使得以点D、A、B、C为顶点的四边形是平行四边形，请写出点D的坐标为（3，2）（-3，2）（5，-2）．
分析 需要分类讨论：以AB为边的平行四边形和以AB为对角线的平行四边形．
解答 
解：如图，①当BC为对角线时，易求M1（3，2）；
②当AC为对角线时，CM∥AB，且CM=AB．所以M2（-3，2）；
③当AB为对角线时，AC∥BM，且AC=BM．则|My|=OC=2，|Mx|=OB+OA=5，所以M3（5，-2）．
综上所述，符合条件的点D的坐标是M1（3，2），M2（-3，2），M3（5，-2）．
故答案为：（3，2）（-3，2）（5，-2）．
点评 本题考查了坐标与图形的性质，平行四边形的判定与性质．解题时，注意分类讨论，以防错解或漏解．
练习册系列答案
相关题目
如图，在平面直角坐标系中，⊙P的圆心坐标是（3，a）（a＞3），半径为3，函数y=x的图象被⊙P截得的弦AB的长为4$\sqrt{2}$，则a的值是3+$\sqrt{2}$．