题目内容
8.解不等式组:(1)$\frac{2x-1}{3}$-$\frac{10x+1}{6}$≥$\frac{5}{4}$x-5
(2)$\left\{\begin{array}{l}{x+2(x-1)<4}\\{\frac{1+4x}{3}>x-1}\end{array}\right.$.
分析 (1)利用解不等式的步骤与方法与不等式的性质求得解集即可;
(2)分别求出两个不等式的解集,再求其公共解集.
解答 解:(1)$\frac{2x-1}{3}$-$\frac{10x+1}{6}$≥$\frac{5}{4}$x-5
4(2x-1)-2(10x+1)≥15x-60
8x-20x-15x≥-60+4+2
-27x≥-54
x≤2;
(2)$\left\{\begin{array}{l}{x+2(x-1)<4}\\{\frac{1+4x}{3}>x-1}\end{array}\right.$
解不等式①得x<2
解不等式②得x>-4
不等式组的解集为-4<x<2.
点评 本题考查一元一次不等式组的解法,求不等式组的解集,要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
19. 如图,在平行四边形ABCD中,对角线AC、BD相交于点O.如果BD=12,AC=10,BC=m,那么m的取值范围是( )
如图,在平行四边形ABCD中,对角线AC、BD相交于点O.如果BD=12,AC=10,BC=m,那么m的取值范围是( )
 如图,在平行四边形ABCD中,对角线AC、BD相交于点O.如果BD=12,AC=10,BC=m,那么m的取值范围是( )
如图,在平行四边形ABCD中,对角线AC、BD相交于点O.如果BD=12,AC=10,BC=m,那么m的取值范围是( )| A. | 10<m<12 | B. | 2<m<22 | C. | 1<m<11 | D. | 5<m<6 |
13.若a-b=$\sqrt{2}$-1,ab=$\sqrt{2}$,则代数式(a-1)(b+1)的值等于( )
| A. | 2$\sqrt{2}$+2 | B. | 2$\sqrt{2}$-2 | C. | 2$\sqrt{2}$ | D. | 2 |
 如图,正方形ABCD和正方形CEFG中,点D在CG上,已知:BC=1,CE=7,H是AF的中点,则AF=10,CH=5.
如图,正方形ABCD和正方形CEFG中,点D在CG上,已知:BC=1,CE=7,H是AF的中点,则AF=10,CH=5.
 如图,∠AEF+∠CFE=180°,∠1=∠2,EG与HF平行吗?为什么?
如图,∠AEF+∠CFE=180°,∠1=∠2,EG与HF平行吗?为什么?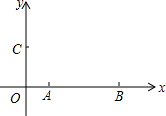 如图,在平面直角坐标系中,点A的坐标为(1,0),点B的坐标为(4,0),点C在y的正半轴上,且OB=2OC,在直角坐标平面内确定点D,使得以点D、A、B、C为顶点的四边形是平行四边形,请写出点D的坐标为(3,2)(-3,2)(5,-2).
如图,在平面直角坐标系中,点A的坐标为(1,0),点B的坐标为(4,0),点C在y的正半轴上,且OB=2OC,在直角坐标平面内确定点D,使得以点D、A、B、C为顶点的四边形是平行四边形,请写出点D的坐标为(3,2)(-3,2)(5,-2).