题目内容
13．在下列6个图形中，每个小四边形都是全等的正方形，那么沿其正方形相邻边折叠，能够围成正方体的编号是（ ）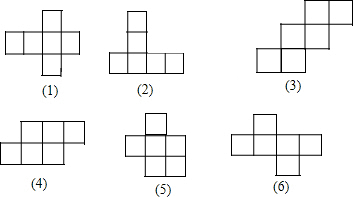
| A． | ①②③④ | B． | ①②⑥ | C． | ①③④ | D． | ①③⑥ |
分析 由平面图形的折叠及正方体的表面展开图的特点解题．
解答 解：（1）（3）（6）折叠后能围成一个正方体，符合题意；
（2）折叠后，有两个面重合，不能折成正方体，不符合题意；
（4）（5）出现了“田”字格，故不能折成正方体，不符合题意．
故选D．
点评 本题考查了展开图折叠成几何体，解题时勿忘记四棱柱的特征及正方体展开图的各种情形．注意：只要有“田”字格的展开图都不是正方体的表面展开图．
练习册系列答案
相关题目
3．
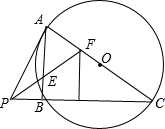如图，已知：PA切⊙O于A，若AC为⊙O的直径，PBC为⊙O的割线，E为弦AB的中点，PE的延长线交AC于E，且∠FPB=45°，点F到PC的距离为5，则FC的长为（ ）
如图，已知：PA切⊙O于A，若AC为⊙O的直径，PBC为⊙O的割线，E为弦AB的中点，PE的延长线交AC于E，且∠FPB=45°，点F到PC的距离为5，则FC的长为（ ）| A． | 10 | B． | 12 | C． | $5\sqrt{5}$ | D． | $5\sqrt{6}$ |
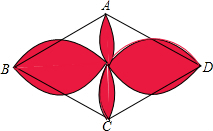如图，四边形ABCD是菱形，AB=10cm，∠ABC=60°，分别以ABCD的四条边为直径作半圆．求图中红色部分的面积．
如图，四边形ABCD是菱形，对角线AC与BD相交于点0，∠ACD=30°，BD=2．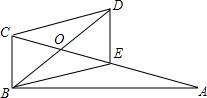
如图，△ABC是直角三角形，且∠ABC=90°，四边形BCDE是平行四边形，E为AC的中点，BD平分∠ABC，求$\frac{OC}{OD}$的值．
3．若a＜b＜0，化简$\root{3}{{{{（{a-b}）}^3}}}-\sqrt{{{（{a-b}）}^2}}+\root{3}{a^3}-\sqrt{b^2}$的结果为（ ）
| A． | 3a-b | B． | 3（b-a） | C． | a-b | D． | b-a |