题目内容
已知点(3,5)在直线y=ax+b(a,b为常数,且a≠0)上,则5(3a+b)的值为 .
考点:一次函数图象上点的坐标特征
专题:
分析:把点的坐标代入直线解析式得到3a+b=5,然后代入所求代数式进行计算即可得解.
解答:解:∵(3,5)在直线y=ax+b上,
∴3a+b=5,
∴5(3a+b)=5×5=25.
故答案为:25.
∴3a+b=5,
∴5(3a+b)=5×5=25.
故答案为:25.
点评:本题考查了一次函数图象上点的坐标特征,求出a、b的关系式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
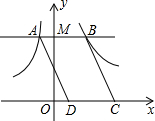 如图,过y轴上一个动点M作x轴的平行线,交双曲线y=-
如图,过y轴上一个动点M作x轴的平行线,交双曲线y=-| 4 |
| x |
| 10 |
| x |
| A、7 | B、10 | C、14 | D、28 |
若抛物线y=x2-2x+c与y轴的交点为(0,-3),则下列说法不正确的是( )
| A、抛物线开口向上 |
| B、抛物线与x轴的交点为(-1,0),(3,0) |
| C、当x=1时,y的最大值为-4 |
| D、抛物线的对称轴是直线x=1 |
 观察下面有※组成的图案和算式:
观察下面有※组成的图案和算式: 如图,将一张长方形纸片ABCD沿EF折叠,ED′与BC交于点为G,点D、点C分别落在点D′、点C′的位置上,若∠EFG=60°,则∠1=
如图,将一张长方形纸片ABCD沿EF折叠,ED′与BC交于点为G,点D、点C分别落在点D′、点C′的位置上,若∠EFG=60°,则∠1=